Математична статистика - Руденко В. М. - Нормальний розподіл

Роботи Я. Бернуллі, а також приватні дослідження інших математиків XVII-XVIII ст. з Європи згодом оформилися в теорію ймовірності. У початковий період розвитку основною проблемою даної теорії було визначення ймовірності складної події при нагоді певної кількості незалежних появ на зразок розглянутих вище випробувань з підкиданням монет. Формула для таких завдань була визначена, проте для великих обсягів (наприклад, обчислити ймовірність того, що при 20 000 підкидань монети випадуть 5000 або більше "гербів") такі обчислення виглядали дуже громіздкими.

На початку XVIII ст. де Муавру (1667-1754) вдалося апроксимувати біноміальний розподіл за допомогою формули

F (x) = -)= ехрі - (3.57)

Де Fx) - ймовірність; fi і а - середнє і стандартне відхилення. Функція Fx) отримала назву щільності нормального розподілу.

Функція нормального розподілу визначається через щільність

Ф( x) =| f (t)dt. (3.58)

-сс

MS Excel містить функцію =НОРМРАСП(х; /г; а; І), яка повертає значення або функції Ф(х), або функції щільності Fx) для заданих fi і а. Параметр І визначає форму функції: якщо 1=0, =НОРМРАСП() повертає значення Ф(х), інакше fx). На рис. 3.42 приведено формули розрахунку розподілів з використанням функцій MS Excel =БИНОМРАСП() і =НОРМРАСП().

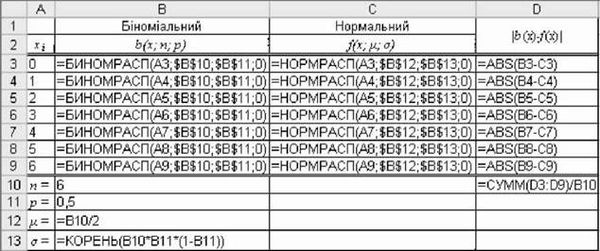
Рис. 3.42. Формули розрахунку розподілів (п = 6;р = 0,5; ¡1 = 3; а = 1,22)

На рис. 3.43 і 3.44 представлено результати розрахунку щільності біноміального і нормального розподілів і відповідні графіки для двох наборів параметрів: перший (п = 6;Р = 0,5; /г = 3; А = 1,22) і другий (п = 10;р = 0,5; /г = 5 і а = 1,58). Значення/г і а отримано з біноміального розподілу.

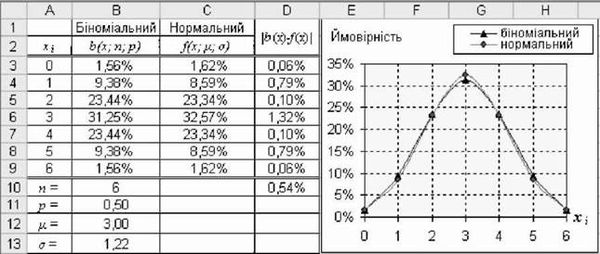
Рис. 3.43. Біноміальний і нормальний розподіли (п = 6;р = 0,5; ¡1 = 3; а =1,22)

Порівнюючи графіки кривих біноміального і нормального розподілів, можна констатувати, що функція нормального розподілу цілком задовільно апроксимує функцію біноміального розподілу. Більш того, із збільшенням обсягу вибірки П відхилення значень нормального і біноміального розподілів ХЬ(х)-Дх)| /п зменшується (для п = 6 складає 0,54% ; для п = 10 - 0,24%).

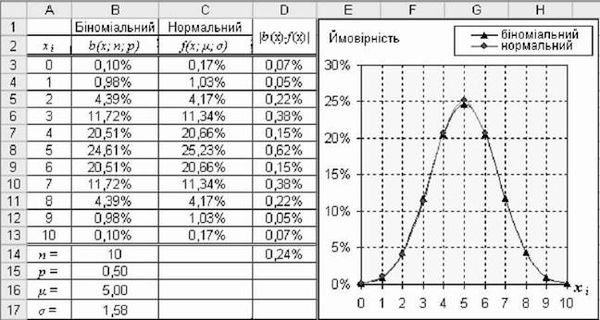
Рис. 3.44. Біноміальний і нормальний розподіли (п =10;р = 0,5; /г=5; а = 1,58)

Універсальність функції щільності нормального розподілу полягає в тому, що вона використовує у якості своїх аргументів одні з основних характеристик сукупностей - середнє Р і стандартне відхилення а, а також "працює" і для дискретних, і для неперервних величин.

Формула щільності нормального розподілу (3.56) задає лише деяку типову форму графіка у вигляді симетричного "дзвону", відомого під назвою нормальної кривої. Міняючи значення /г і а, можна зрушувати конкретну нормальну криву вздовж числової осі ординат і міняти її розмах.

На рис. 3.45 графіки нормальних розподілів побудовано для сукупностей, які мають різні середні /г і різні стандартні відхилення а. Пропонуємо проаналізувати схожість і різницю цих розподілів щільності.

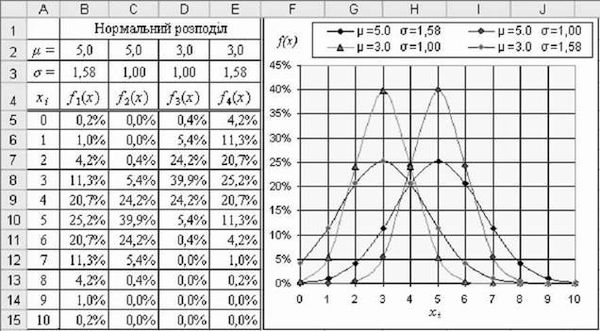
Рис. 3.45. Сім'я графіків щільності нормального розподілу Популярність нормального розподілу обгрунтовано висновками центральної граничної теореми, оскільки в природі, соціальній, педагогічній сферах і ситуаціях багато випадкових величин є сумами декількох випадкових факторів. Серед сімейства нормальних розподілів особливе місце займає розподіл, який має нульове середнє Fi = 0 і одиничне стандартне відхилення а = 1

F (z) = ^Lexp{- І (3.59)

Графік відповідного розподілу називається стандартним нормальним розподілом. Значення і функції щільностіf z), і розподілу Ф(г) можна отримати за допомогою або спеціальних таблиць18, або комп'ютерних програм, зокрема, функцій MS Excel =НОРМРАСП() і =НОРМСТРАСП() (див. рис. 3.46).

Стандартному нормальному розподілові притаманні такі властивості:

O площа, яка має сенс ймовірності під графіком щільності, дорівнює 1;

O крива графіку не перетинає вісь z хоча і наближається до неї у міру того, як Z стає більше трьох, але ніколи її не торкається;

O найвища точка кривої щільності розподілу 0,3989 розташована над нульовим значенням z ;

18 Болыпев Л. Н., Смирнов Н. В. Таблицы математической статистики. - М.: Наука, 1965 (1-е изд.), 1968 (2-е изд.), 1983 (3-е изд.).

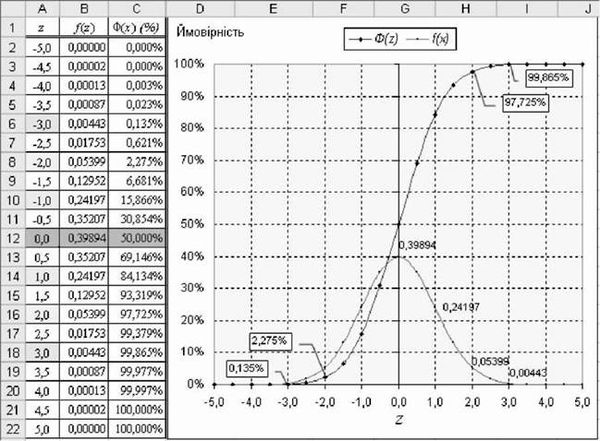
Рис. 3.46. Значення і графіки стандартного нормального розподілу

O стандартна нормальна крива завжди буде симетричною щодо вертикалі, проведеної через і = 0, її асиметрія і ексцес дорівнюють нулю;

O всяку іншу нормальну криву можна сумістити із стандартною за допомогою операції Нормалізації (перехід від змінної х до і див. розділ 2.2 )

І, =^~^; (3.60)

O якщо випадкові величини X 1 і Х2 мають функції нормального розподілу И(р1; сі) і N(^2; (72) відповідно, то випадкова величина (X 1 + Х2) має нормальний розподіл N (/^ + ^2 ;д/ег2 +<т2);

O якщо випадкові величини Х1, Х2, ХП є незалежними і мають один той

_ Х + Х + + Х

Самий розподіл N(м; о), то їхнє середнє арифметичне Х = -1-2----

П

Має нормальний розподіл N(¿1; <у і4п).

Як відомо, площа під кривою функції щільності має сенс ймовірності. Загальна площа під нормальною кривою, де абсциса х змінюється від - оо до + оо, дорівнює 1. А це значить, що ймовірність р того, що х будуть приймати будь які значення (від - оо до + оо), дорівнюватиме 1 (або 100%).

Ймовірність того, що х прийматиме значення від Х1 до Х2, дорівнюватиме значенню відповідної Площі під нормальною кривою, обмежену з боків цими значеннями. Для нормованої нормальної кривої (де а =1) значення х можна записувати в одиницях стандартного відхилення А, наприклад "х змінюється від -1а до +1о", або "х змінюється від -1 до +1".

Для значень х від -1а до +1(7 площа (і відповідна ймовірність приймати значення /і ± а) дорівнюватиме 0,683 (або ймовірність 68,3%).

Для значень х від -2а до +2(7 площа (і відповідна ймовірність приймати значення /і ± 2а) дорівнює 0,954 (або 95,4%).

Для значень х від -3а до +3а площа (і відповідна ймовірність) дорівнює 0,997 (або 99,7%). Слід звернути увагу на те, що 99,7% значень сукупності (тобто практично всі її значення) знаходяться в межах середнього /г ± 3а. Цей факт отримав своєрідну назву "закон трьох сигм".

Як отримати значення ймовірностей з використанням нормального розподілу? Поряд з класичними формулами, які виглядають занадто громіздкими і дуже незручними, існують спеціально розраховані статистичні таблиці. Проте найпотужнішим способом вважаються комп'ютерні засоби.

Щоб підрахувати ймовірність (площу), наприклад, для значень Х від -1а до +1(7 , необхідно виконати 3 дії:

O визначити ймовірність р1 для х від - оо до -1а за допомогою функції =НОРМРАСП(-1; 0; 1; 1), яка поверне значення 15,866%;

O визначити ймовірність р2 для х від - оо до +1(7 за допомогою функції =НОРМРАСП(+1; 0; 1; 1), яка поверне значення 84,134%;

O визначитир = р2- Рі = 84,134% - 15,866% = 68,269% ~ 68,3%..

В математичній статистиці часто виникає необхідність вирішувати зворотні завдання типу: "визначити х, якому відповідає певна ймовірністьР". Наприклад, для якого значення х, починаючи від ймовірність складатиме 5%?

З математичної точки зору необхідно визначити таке 2, яке обмежує ординатою зліва 5% площі під нормальною кривою (див. рис. 3.47).

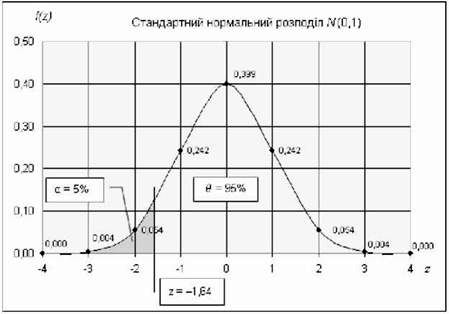
Рис. 3.47. Розподіл N(0,1) має параметр z 0;О5 ~ -1,64

Традиційно це завдання також вирішувалося за допомогою спеціальних статистичних таблиць. Проте, можна запропонувати використовувати функцію MS Excel =НОРМОБР( р; fi; о), яка повертає значення z для заданих ймовірності Р, середнього Fi, стандартного відхилення А. Так, для /><0,05, fi = 0 і а = 1 функція =НОРМОБР(0,05; 0; 1) поверне значення Z ~ -1,64485. Аналогічно для/7<0,01 =НОРМОБР(0,01;0;1) поверне значення Z ~ -2,32635 і т. д.

Для безлічі нормальних кривих, що відрізняються один від одного значеннями Fi і А, важливою загальною властивістю є те, що будь-яка частина площі (яка асоціює ймовірність) під нормальною кривою може бути виражена в середніх Fi і стандартних відхиленнях а. Наприклад, в будь-якому нормальному розподілі приблизно 95% площі під кривою лежить в межах Двох а від середнього Fi (якщо точно визначати, то 95% площі лежить в межах середнього Fi від -1,96с до +1,96ег (див. рис. 3.48);

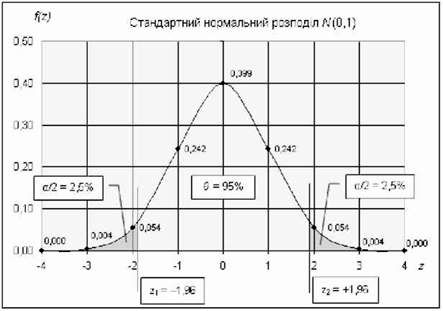
Рис. 3.48. Розподіл N(0,1) має параметр г 0 025| ~ 1,96

Важливість використання в різноманітних педагогічних і психологічних дослідженнях нормального розподілу пояснюється висновками Центральної граничної теореми, яка є фундаментальним проявом закону великих чисел. Між тим в конкретних прикладних задачах нормальність результатів випробувань встановити із загальних міркувань, як правило, не можливо. Нормальність варто перевіряти за допомогою статистичних критеріїв, або ж використовувати непараметричні методи (див. розділ 5.3).

Схожі статті




Математична статистика - Руденко В. М. - Нормальний розподіл

Предыдущая | Следующая