Математична статистика - Руденко В. М. - Розподіли "хі-квадрат", Стьюдента і Фішера

При побудові статистичних моделей нормальному законові безумовно належить центральне місце. Проте намагання використовувати його для моделювання розподілу емпіричних даних у будь-якому разі не завжди є обгрунтованими. Більш істотно те, що багато методів обробки даних засновано на розрахункових величинах, що мають хоча й інші, але близькі розподіли до розподілу нормального. Крім того, за допомогою нормального закону визначаються широко розповсюджені в математичній статистиці розподіли х2 (хі-квадрат), і Стьюдента і Б Фішера.

Розподіл /2 (хі-квадрат) - це розподіл випадкової величини

X = X2 + X22 + ... + XN2, (3.61)

Де випадкові величини X1, X2, XN є незалежними і мають той самий стандартний нормальний розподіл N(0,1). Кількість доданків П називається "числом ступенів вільності" розподілу хі-квадрат.

Розподіл І Стьюдента - це розподіл випадкової величини

Т=% (3.62)

Де випадкові величини и і X незалежні, и має стандартний нормальний розподіл N(0,1), а X - розподіл хі-квадрат з п ступенями вільності. При цьому П називається "числом ступенів вільності" розподілу Стьюдента.

Розподіл Б Фишера - це розподіл випадкової величини

Б = К-, (3.63)

Де випадкові величини Х1 і Х2 - незалежні і мають розподіли хі-квадрат з числом ступенів вільності к1 і к2 відповідно.

Отже, розподіли х2 (хі-квадрат), ї Стьюдента і Б Фішера є похідними від нормального закону. Розглянемо властивості цих розподілів докладніше.

Розподіл /2 "хі-квадрат" Можна отримати за схемою повторних випробувань, якщо з генеральної сукупності нормально розподілених значень з нульовим середнім (м=0) і одиничним стандартним відхиленням (о=1) випадковим методом вилучати незалежно п значень X1, X2, XN, а потім розраховувати суму їх квадратів (X1)2 + (X2)2 + ". + (X,,)2. У результаті багаторазових випробувань значення цих сум будуть мати розподіл Хп2 (хі-квадрат) з п степенями вільності. Аналітична форма запису щільності розподілу Хп2 має вигляд:

^Хп) = П 1 /П Х21 oЕ (3.64)

Де /У2 (х, п) - функція щільності розподілу х2; п - число ступенів вільності; Г() - гама-функція, яка зручно розраховується в Excel за допомогою виразу =EXP(rAMMAbMOr()). ФункціяF Х2 (x, и)>0 для x > 0 і f Х2 (x, и)=0 для x<0.

На рис. 3.49. показано розрахунки значень і графіки щільності розподілу ^2 для трьох ступенів вільності (2; 3 і 5).

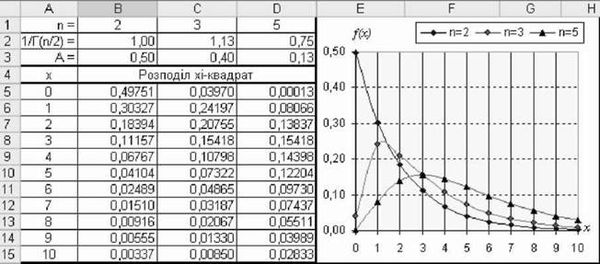
Рис. 3.49. Розрахунки і графіки щільності розподілу %

Для розрахунку розподілу х 3 числом ступенів вільності, наприклад, п=2 необхідно внести:

O у комірку В2 вираз =1ІЕХР(ГАММАНЛОГ(Б$1І2));

O у комірку В3 вираз =Б2І2Л(Б$1І2);

O у комірку В5 вираз =Б$3*$А5Л(Б$1І2-1)*ЕХР(-$А5І2);

O у комірки В6:В15 - аналогічні вирази.

У стовпчиках С і Б розраховано значення розподілу Х для числа ступенів вільності п=3 і п=5.

Як видно з графіків, при збільшенні числа ступенів вільності П розподіл % наближається до нормального розподілу з середнім П і стандартним відхиленням л/2й. Якщо дисперсію можна записати як суму квадратів П незалежних випадкових значень випробувань Х1, Х2, ХП, наприклад,

'І = Л (ІХ,2 - пХ2) = (Х2 + Х2 + ...+Х2) - ^,

П -1 ,-=1 п -1 п -1

То величина 8Х2 може мати розподіл /2". Тому природно, що розподіли х використовують у статистичних висновках щодо дисперсій (див. розділ 5.4) .

Розподіл і Стьюдента. Властивості нормального розподілу можна використовувати лише тоді, коли обсяг вибірки п є "достатньо великим" - на це звертає увагу Центральна гранична теорема. Проте в реальних умовах обсяг вибірки, як правило, не є "достатньо великим". У цих умовах використовують інші розподіли. Одним із найважливіших вважається розподіл Стьюдента:

Г'(Х, П) = ^ГП ^ + Т ] , (3.65)

Де /і(х, п) - функція щільності розподілу Стьюдента; п - число ступенів вільності; Г() - гама-функція.

На рис. 3.50. показано розрахунки розподілу Стьюдента для ступенів вільності (1; 2 і 8) і для порівняння відповідні значення нормального розподілу.

Для розрахунку щільності розподілу Стьюдента з числом ступенів вільності п=1 необхідно внести:

O у комірку В2 вираз =ЕХР(ГАММАНЛОГ((Б$1+1)/2));

O у комірку В3 вираз =ЕХР(ГАММАНЛОГ(Б$1/2));

O у комірку В4 вираз =В2/В3/КОРЕНЬ(Б$1*ПИ());

O у комірку В7 вираз =В$4*(1+$А7Л2/В$1)Л(-(В$1+1)/2);

O у комірки В8:В19 внести аналогічні вирази;

У стовпчиках С і Б розраховано значення розподілу Стьюдента для числа ступенів вільності п=2 і п=8. У стовпчику Е - значення щільності нормального розподілу, для чого, наприклад, у комірку Е7 слід внести вираз =НОРМРАСП(А7;0;1;0).

Розподіли Стьюдента для трьох ступенів вільності (1; 2 і 8) можна розрахувати за допомогою функції =СТЬЮДРАСП(). Так, у комірку Р7 необхідно внести =СТЬЮДРАСП(АВ8($А7);Р$1;1), аналогічні вирази внести у комірки Р8:Р13. У комірку Б14 внести =1-СТЬЮДРАСП(АВ8($А14);Р$1;1), аналогічні вирази внести у комірки Р15:Р19. Такі ж дії провести у стовпчиках в і Н.

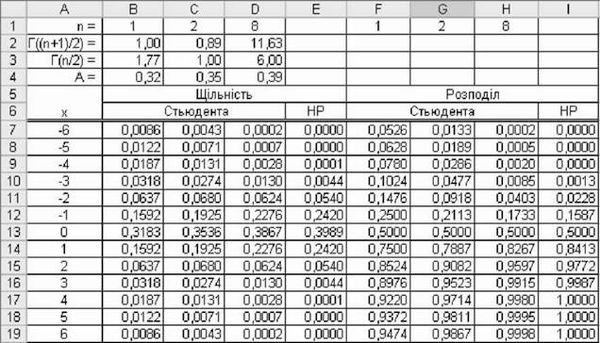
Рис. 3.50. Значення розподілів Стьюдента і розподілу N(0,1)

Для розрахунку нормального розподілу у комірку 17 внести вираз =НОРМРАСП(Л7;0;1;1), аналогічні вирази внести у комірки 18:119.

На рис. 3.51. показано сімейство графіків розподілу Стьюдента для трьох ступенів вільності (1; 2; 8), а також графік стандартного нормального розподілу N(0,1).

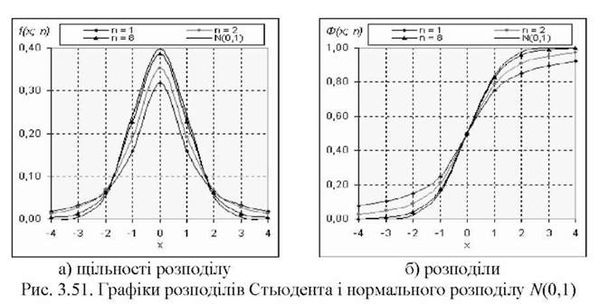
Як видно, при збільшенні числа ступенів вільності П розподіли Стьюдента асимптотично наближаються до нормального розподілу. Коли обсяг вибірки п стає "достатньо великим", тобто практично П -" со, розподіли Стьюдента збігаються з нормальним розподілом. Найчастіше розподіли Стьюдента використовують у статистичних висновках щодо Середніх (див. розділ 5.4).

Розподіл Б Фішера можна отримати, використовуючи схему повторних випробувань, коли з генеральної сукупності нормально розподілених значень з параметрами (м=0 і о=1) випадковим методом спочатку формують першу змінну Х1 з розподілом "хі-квадрат" і степенями вільності п, а потім незалежним шляхом формують другу змінну Х2 з розподілом "хі-квадрат" і степенями вільності т. Нова випадкова величина, що має властивості розподілу Фішера, складатиметься з відношення

Р = Х±/ Х±. (3.66)

П / Т

Функція щільності розподілу Фішера має вигляд

Де /Р (х, п, т) - функція щільності розподілу Фішера; П і Т - число ступенів вільності; Г() - гама-функція.

На рис. 3.52. показано розрахунки і графіки щільності розподілу Фішера для трьох наборів ступенів вільності п і т (2 і 3; 5 і 4; 20 і 4 відповідно).

Для розрахунку розподілу Фішера, наприклад, з числом ступенів вільності п=2 і т=3 необхідно внести:

O у комірку В3 вираз =ЕХР(ГАММАНЛОГ((Б$1+Б$2)І2));

O у комірку В4 вираз =ЕХР(ГАММАНЛОГ(Б$1І2));

O у комірку В5 вираз =ЕХР(ГАММАНЛОГ(Б$2І2));

O у комірку В6 вираз =Б3ІБ4ІБ5*(Б$2ІБ$1)Л(Б$2І2);

O у комірку В7 вираз =Б$6*$Л8Л(Б$2І2-1)*(1+Б$2ІБ$1*$Л8)Л(-(Б$2+Б$1)І2);

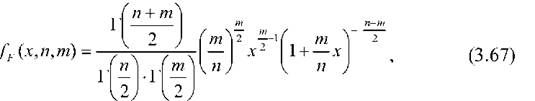
O у комірки В8:В18 - аналогічні В7 вирази.

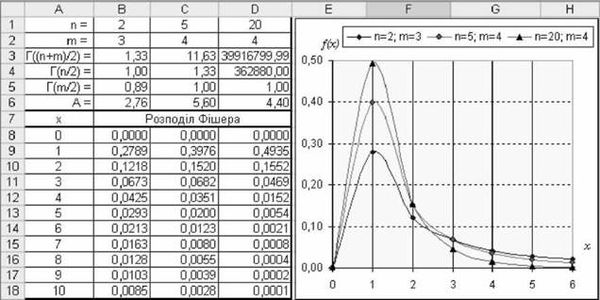
Рис. 3.52. Значення і графіки щільності розподілу Фішера

У стовпчиках С і D розраховано значення розподілу Фішера для інших наборів числа ступенів вільності n і m. З рис. 3.52. видно, що при збільшенні числа ступенів вільності n і m розподіл Фішера наближається до нормального розподілу з середнім m/(n-2). Функція fF (x, n, m)>0 для x>0 і FF (x, n, m) = 0 для x <0. Розподіл Фішера є теоретичною базою дисперсійного аналізу, що базується на зіставленні дисперсій вибірок випадково витягнутих із нормальної сукупності, відношення яких складає F-критерій Фішера: F=s//s22, де sj2 і s22 - дисперсії першої і другої вибірок (див. розділ 5.4).

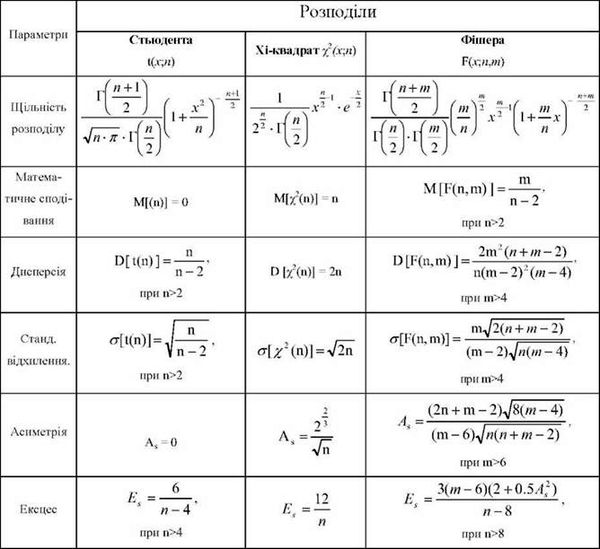
Для порівняння властивостей розподілів "хі-квадрат", Стьюдента і Фішера їхні характеристики представлено в табл. 3.8.

На властивостях нормального розподілу, розподілів Стьюдента, Фішера хі-квадрат побудовано математичні методи статистичного оцінювання, перевірки статистичних гіпотез, дисперсійний аналіз та ін. (див. розділи 5 і 6). Таблиці значень цих розподілів можна знайти в спеціальній літературі або скористатися відповідними функціями MS Excel, зокрема: =НОРМРАСП(), =НОРМСТРАСП(), =ХИ2РАСП(), =СТЬЮДРАСП(), =FPACn().

Таблиця 3.8

Характеристики розподілів

Запитання. Завдання.

1. Про що стверджує теорема Бернуллі?

2. При яких умовах "працює" біноміальний розподіл?

3. Який вигляд мають графіки диференціального та інтегрального біноміального розподілу?

4. Яка основна ідея загальної методики використання теоретичних функцій на прикладі біноміального розподілу в рішенні реальних завдань?

5. Розкрийте особливості функцій щільності нормального розподілу і функції нормального розподілу.

6. Охарактеризуйте стандартний нормальний розподіл.

7. Чим відрізняються розподіли Стьюдента, Фішера і "хі-квадрат" від нормального розподілу?

8. Повторіть математичні процедури завдань за прикладом 3.19.

9. Виконайте лабораторну роботу № 8.

Схожі статті




Математична статистика - Руденко В. М. - Розподіли "хі-квадрат", Стьюдента і Фішера

Предыдущая | Следующая