Математична статистика - Руденко В. М. - Критерій Лемана-Розенблатта w2 n, m

Непараметричний критерій Лемана-Розенблатта типу омега-квадрат застосовується для перевірки однорідності двох незалежних вибірок. Як і за методом Вілкоксона-Манна-Вітні, елементи першої і другої вибірки, що взято з невідомих розподілів. РП(х) і ЄТ(х), об'єднуються. Для об'єднаної упорядкованої за зростанням вибірки х1, х2, хП, у1, у2, уТ визначаються ранги

RX1, RX2, ^хп, Р-уЬ RY2, ^уш.

Висувається нульова гіпотеза однорідності Н0: ГП(х) = ЄТ(х) проти альтернативної гіпотези Н}: БП(х) Ф ЄТ(х).

Статистика критерію Лемана-Розенблатта визначається формулою

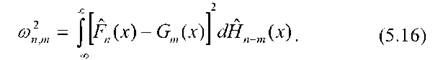
Де ГП (х) і ОТ (х) - емпіричні функції розподілу вибірок обсягами П і т, " п ~ т "

Н...... (х) =-Р'П (х) н--СП (х) - емпірична функція об'єднаної вибірки.

П + т п + Т

Значення статистики залежить лише від рангів елементів вибірки:

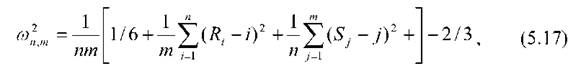
Де ЛІ - ранг х(і), 8у - ранг у0) в об'єднаній варіаційній вибірці. Критерій має однобічну (праву) критичну область. При потраплянні зна-Пт 2

Чення статистики П ^ Т АП, т у напівінтервал (71-а, да}, гіпотеза Н0 відхиляється. Значення деяких основних квантилів наведено у табл. 5.2.

Таблиця 5.2

А =

0,5 0,15

0,1

0,05 0,025

0,01

0,001

1-а =

0,12 0,28

0,35

0,46 0,58

0,74

1,17

Для незначних за обсягом вибірок (п, т > 7) використовується нормована статистика

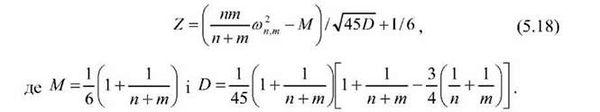
Приклад 5.9. За допомогою критерію Лемана-Розенблатта перевірити гіпотезу щодо однорідності вибірок (за даними прикладу 5.5). Послідовність рішення:

O Формулювання гіпотез:

Н0: відмінності у вибіркових показниках Не є статистично значущі; Н1: відмінності у вибіркових показниках Є статистично значущі.

O Розрахунки емпіричного критерію (рис. 5.22 і 5.23):

- присвоїти ім'я "Виб1" і "Виб2" двом вибіркам (див. розрахунки V-Критерію);

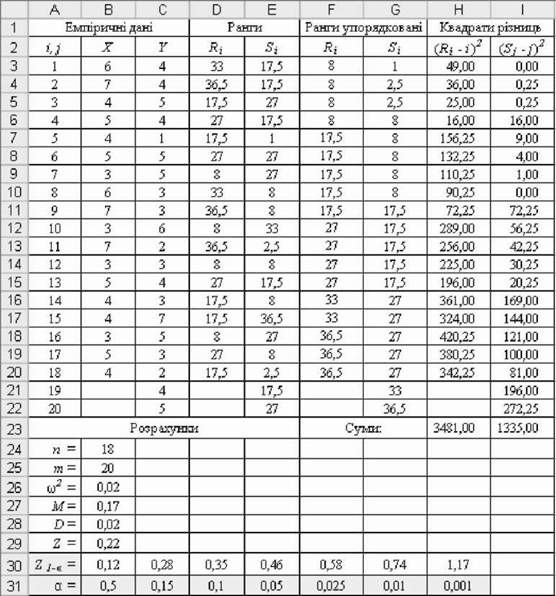
Рис. 5.22. Результати розрахунків критерію ю2

- у стовпчиках б і е отримати ранги значень вибірок, розглядаючи їх як одну об'єднану групу, приписуючи меншому значенню нижчий ранг (загальна кількість рангів п + т). Для цього внести у стовпчики ЛІ і 5 відповідний вираз, який, наприклад, для комірки б3 виглядатиме як:

=(СЧЕТ(Виб1:Виб2) + 1 - РАНГ(в3;Виб1:Виб2; 1) -

- РАНГ(в3;Виб1:Виб2; 0))/2+РАНГ(в3;Виб1:Виб2;1);

- скопіювати цей вираз в інші комірки стовпчиків б і е, отримати ранги;

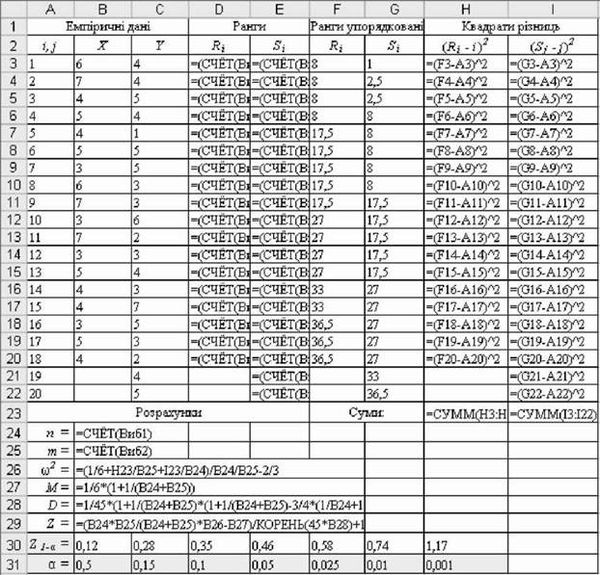
Рис. 5.23. Розрахункові формули критерію ю2

- скопіювати за допомогою команд головного меню MS Excel [Правка -> Спеціальна вставка...] значення рангів у комірки стовпчиків F і G, упорядкувати ранги за зростанням;

- у комірках Н2:І22 розрахувати квадрати різниць (R - і)2 і (S-jj2;

- у комірках Н23 і 123 розрахувати суми квадратів різниць £(R - і)2 і

Z(Sj-j)2 0;

- розрахувати обсяги вибірок n і m, критерій ю2 (5.17), параметри M, D і Z (5.18), а також значення емпіричної нормованої статистики Z ~ 0,22.

O Визначити критичне значення Z1-a за табл. 5.2 для a = 0,05. Квантиль Z0,95 = 0,46.

O Прийняття рішення. Оскільки Z

На основі порівняльного аналізу критеріїв можна зробити такі висновки.

1) Область застосувань методу перевірки однорідності за допомогою критерію Стьюдента обмежена. Він дозволяє перевіряти гіпотезу про рівність математичних очікувань, але не гіпотезу про те, що обидві вибірки взяті з однієї й тієї ж генеральної сукупності. Класичні умови застосовності критерію Стьюдента в переважній більшості психолого-педагогічних і інших завдань не виконуються. При значних і приблизно рівних обсягах вибірок його можна застосовувати. При кінцевих обсягах вибірок традиційний метод носить досить наближений характер.

2) Застосування критерію Крамера-Велча не менш обгрунтовано, чим застосування критерію Стьюдента. Додаткова перевага - не потрібно контролювати вимоги рівності дисперсій. Тому представляється доцільним замінити використання критерію Стьюдента на критерій Крамера-Велча.

3) При зіставленні двох емпіричних розподілів за критерієм Колмогоро-ва-Смірнова необхідно, щоб обсяги вибірок були п1? п 2 > 50, при зіставленні емпіричного розподілу з теоретичним допускається при п>5. Розряди мають бути впорядковані за зростанням (спаданням) ознаки.

4) Критерій Вілкоксона-Манна-Вітні є одним із найбільш розповсюджених непараметричних рангових критеріїв, що використовується для перевірки однорідності двох вибірок. Проте у варіанті загальної альтернативи критерій не є спроможним, тому рекомендують застосовувати спроможні критерії, зокрема, критерій Лемана-Розенблатта типу омега-квадрат.

Отже, для перевірки однорідності функцій розподілу рекомендують застосовувати статистику Лемана-Розенблатта типу омега-квадрат. Для перевірки однорідності математичних очікувань доцільно застосовувати критерій Крамера-Велча. Статистики Стьюдента, Вілкоксона-Манна-Вітні та ін. припустимо використовувати лише в окремих випадках [49].

Запитання. Завдання.

1. Чому область застосувань методу перевірки однорідності за допомогою критерію Стьюдента обмежена?

2. Коли доцільно застосовувати критерій Стьюдента і?

3. Обгрунтуйте доцільним заміну використання критерію Стьюдента на критерій Крамера-Велча.

4. Які існують обмеження при зіставленні двох емпіричних розподілів за критерієм Колмогорова-Смірнова?

5. Проаналізуйте критерії Вілкоксона-Манна-Вітні і Лемана-Розенблатта, які використовується для перевірки однорідності двох вибірок

6. Повторіть математичні процедури завдань за прикладами 5.5 і 5.9.

7. Виконайте лабораторні роботи № 11 і № 12.

Схожі статті




Математична статистика - Руденко В. М. - Критерій Лемана-Розенблатта w2 n, m

Предыдущая | Следующая