Математична статистика - Руденко В. М. - Умовна ймовірність

Якщо подія А відбувається у випробувані, яке обмежене додатковими умовами здійснення події В, то міра можливості події А визначається Умовною ймовірністю р(а | Б). Отже, умовною ймовірністю Р(а | Б) називається ймовірність події А, обчислена за умови, що подія В вже відбулася.

Умовна ймовірність має сенс для залежних подій. Для незалежних подій А і В умовна ймовірність перетворюється на звичайну:

Р(А | Б) = Р(А), або Р(Б | А) = Р(Б).

Отже Незалежні події (за означенням) не змінюють ймовірності появи іншої.

Ймовірність добутку залежних подій А і В визначається за формулою:

Р(А ■ В) = Р(а | Б) o Р(Б). (3.5)

Умовна ймовірність Р^В) як ймовірність здійснення події А за умови, що подія В відбулася, тобто р(В) > 0, визначається з (3.5):

Р(А | Б) = Р(А'В) . (3.6)

^ і > р(б) ^ >

Для Незалежних подій формула спрощується і приймає вже відомий вигляд:

Р( А ■ В) = Р( А) o Р( В).

Приклад 3.4. В академічній групі 15 хлопців і 10 дівчат. Яка ймовірність того, що двоє навмання і підряд вибраних студентів виявляться дівчатами?

Рішення: Загальна бажана подія А (вибір навмання двох студентів-дівчат) складається з добутку двох подій: В1 (випадковий вибір однієї дівчини) і _82 (випадковий вибір ще однієї дівчини), тобто Р(А) = Р(В1 o В2). Ймовірність події В1 - Р(В1). Настання події _82 відбувається після події В1 і оцінюється умовною ймовірністю Р(В2 | В1). Ймовірність добутку залежних подій В1 і _82 дорівнює: Р(В1 o В2) = Р(В1) o Р(В2 | В1).

Ймовірність події В1 визначається як відношення кількості дівчат (10) до

Загальної кількості студентів (10+15), тобто Р(В1) = = 0,4.

Настання події В1 змінює умови для оцінки ймовірності події _82, а саме: зменшується і кількість дівчат (10-1)=9, і загальна кількість студентів (9+15)=24. Тоді ймовірність події _82 як відношення кількості дівчат (9) до за-

9

Гальної кількості студентів (24) дорівнюватиме Р(В2 | В1) = 9-15 = 0,375.

Звідси ймовірність Р(А) події А складатиме

Р(А) = Р(В1 ■ В2) = Р(В1) o Р(В2 | В1) = 0,4 o 0,375 = 0,15 = 15%.

Відповідь: ймовірність вибору навмання двох студентів-дівчат становить 15%.

Формула повної ймовірності

Припустимо, що простір подій (множина £2) складається з п попарно несумісних подій - підмножин Н1,Н2,Н3,...,НП (див. рис. 3.4).

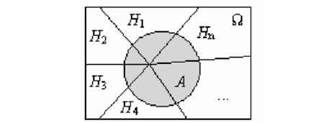
Рис. 3.4. Простір подій {Н1, Н2,..., НП }є£2

З рис. 3.4 видно, що подію А можна уявити як суму добутків події А і кожної з подій Н1,Н2,...,НП (сума перетинів підмножин А з підмножинами Я):

А=А-ИХ+А-ИГ+...+А-ИП = £ А ■ Я,..

Ймовірність події А (за теоремою додавання ймовірностей) визначиться

Р( А) = £Р( А ■ Я,.).

Ймовірність події А (за теоремою множення ймовірностей) визначиться:

Р(А) = ІР(А | Ні) o Р(Н,). (3.7)

¿=1

Вираз (3.7) є формулою повної ймовірності Р(А) події А, якщо подія А залежить від системи подій. Події Н1,Н2,...,НП прийнято називати гіпотезами, за якими може відбутися подія А.

Приклад 3.5. У трьох групах студентів (чисельністю 28, 20 і 25 осіб) відмінники становлять 7, 2 і 5 студентів відповідно. Яка ймовірність того, що навмання вибраний студент є відмінником?

Рішення: Простір подій (множина О.) складається з 3-х попарно несумісних подій - підмножин Н1,Н2,Н3(див. рис. 3.5). Подія А - це результат випробування - вибору навмання студента-відмінника з ймовірністю Р(А).

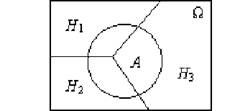
Рис. 3.5. Простір подій {Н1,Н2,Н3}є£2

Ймовірність Р(А) розраховується за формулою повної ймовірності (п=3):

Р(А) = £Р(А |H[) o Р(Я,) = Р( А | o РЯ1) + Р(А | Я2) o Р(Н2) + Р(А | Я3) o Р(Н,).

¿=1

Ймовірність гіпотези Я1 (події про те, що відмінник вибраний з 1-ї групи ):

Р(Я1) =-28-= ^ " 0,38.

28 + 20 + 25 73

Ймовірність гіпотези Я2 (події про те, що відмінник вибраний з 2-ї групи):

Р(Я2) = ---2---- = -2-0 . 0,27. 28 + 20 + 25 73

Ймовірність гіпотези Н3 (події про те, що відмінник вибраний з 3-їгрупи):

25 25

Р(#3) =-25-= - * 0,34.

28 + 20 + 25 73

Умовні ймовірності події А для кожної гіпотези розраховуються як: Р( Л|Я.) = ^ = 0,25; Р( ЛН 2) = ^- = 0,10; Р( ЛН 3) = ^ = 0,20.

28 20 25

За формулою повної ймовірності Р(А) розраховується як:

Р(Л) = Р(Л | Я1) o Р(Я1) + Р(Л | Я2) o Р(Я2) + Р(Л | Я3) o Р(Я3) або

Р(Л) = 0,25 o 0,38 + 0,10o 0,27 + 0,20o 0,34 " 0,095 + 0,027 + 0,068 " 0,19.

Відповідь: ймовірність Р(А) події А про те, що навмання вибраний з трьох груп студент є відмінником, складає приблизно 0,19 або 19%.

Приклад 3.6. В академічній групі з 10 студентів, що прийшли на екзамен, 3 студенти підготовлені відмінно, 4 - добре, 2 - задовільно і 1 - погано. Відмінно підготовлений студент може відповісти на всі 20 питань, добре підготовлений - на 16, задовільно - на 10 питань, погано - на 5 питань. Яка ймовірність того, що навмання викликаний з цієї групи студент відповість на два заданих питання?

Рішення: Простір подій (множина О.) складається з 4-х несумісних подій - підмножин Н1, Н2, Н3, Н 4 (див рис. 3.6).

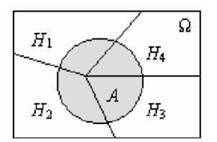
Рис. 3.6. Простір подій {Н1, Н 2, Н 3, Н4}є£1

Подія А - це результат випробування - вибору навмання студента, який успішно відповість на два заданих питання. Р(А) - ймовірність цієї події роз-

Раховується за формулою повної ймовірності (п=4):

Р( А) =Е Р(А|Я,) o Р(Я,).

¿=1

Висуваємо чотири гіпотези щодо ймовірності появи (у результаті виклику навмання) того чи іншого студента з певною підготовкою:

- гіпотеза Н1 : це буде студент, що підготовлений Відмінно, ймовірність його появи Р(Н1) = 3/10 = 0,3;

- гіпотеза Н2 : це буде студент, що підготовлений Добре, ймовірність його появи Р(Н2) = 4/10 =0,4;

- гіпотеза Н3 : це буде студент, що підготовлений Задовільно, ймовірність його появи Р(Н3) = 2/10 = 0,2;

- гіпотеза Н4 : це буде студент, що підготовлений Погано, ймовірність його появи Д#4) = 1/10 = 0,1.

Умовні ймовірності виконання двох завдань студентів з певною підготовкою розраховуються як ймовірності добутку двох залежних подій (подій успішного виконання двох завдань). Згідно з теоремою множення:

- умовна ймовірність виконання двох завдань студентом, що підготовлений Відмінно, дорівнюватиме Р(АН1) = (20/20)-(19/19) = 1;

- умовна ймовірність виконання двох завдань студентом, що підготовлений Добре, дорівнюватиме Д^Яг) = (16/20)-(15/19) ~ 0,63;

- умовна ймовірність виконання двох завдань студентом, що підготовлений Задовільно, дорівнюватиме Р(АЩз) = (10/20)(9/19) ~ 0,24;

- умовна ймовірність виконання двох завдань студентом, що підготовлений Погано, дорівнюватиме Р^НЛ = (5/20)-(4/19) ~ 0,053.

За формулою повної ймовірності Р(А) розраховується як:

Р( А) = Р(А | Я^ ■ Р(Н1) + Р( А | Я2) o РЩ2) + Р( А Щ3) ■ РЩ,) + Р( А | Я4) o РЩЛ)

Або

Р(А) = 1-0,3+0,63-0,4+0,24-0,2+0,053-0,1 = 0,605 = 60,5%. Відповідь: ймовірність Р(А) події А про те, що викликаний навмання студент відповість на два заданих питання, складає приблизно 0,605 або 60,5%.

Схожі статті




Математична статистика - Руденко В. М. - Умовна ймовірність

Предыдущая | Следующая