Логіка - Дуцяк І.3. - ЛЕКЦІЯ 6. Опосередковані виводи. Силогізми
6.1. Силогістичні виводи на підставі традиційної силогістики
Опосередкованими називають виводи, в яких висновок отримують з більш ніж одного засновку. В буквальному сенсі - це виводи, які, на відміну від безпосередніх виводів, містять, крім одного засновку, посередником інші засновки. Одним із видів опосередкованих виводів є силогізми. Теорію так званих категоричних силогізмів (грец.- міркую, роблю висновок) розробив давньогрецький філософ Арістотель (384-322 рр. до н. е.). Суть силогістичних виводів полягає в тому, що на підставі знання відношення першої множини до другої і знання відношення другої множини до третьої визначають відношення першої множини до третьої. Нижче наведено приклад категоричного силогізму. Над рискою - твердження, з яких виводять (засновки), під рискою - твердження, яке отримують унаслідок виведення (висновок):
Усі ссавці е тваринами.
Усі люди е ссавцями.
Усі люди є тваринами.
На підставі знання відношення обсягів між множинами ссавців і тварин, зафіксованого відповідними словами першого засновку, та відношення обсягів множин людей і ссавців, зафіксованого відповідними словами другого засновку, зроблено висновок про відношення між множинами людей і тварин (рис. 6.1):

Рис. 6.1. Суть силогістичних виводів: на підставі відношення кожної з двох множин (люди й тварини) до третьої (ссавці) з'ясовують відношення між цими двома множинами
Фігури та модуси силогізмів
Суб'єкти й предикати тверджень силогізму (засновків і висновків), тобто ті імена, між обсягами яких з'ясовують відношення в силогістичних виводах, називають термінами силогізму.
Структуру силогізму, в якій відтворено розміщення термі-пів у засновках, називають фігурою силогізму. Якщо позначити менший термін (той, який є суб'єктом висновку) символом 5, більший термін (той, який є предикатом висновку) - символом Р, середній термін (той, який міститься в обох засновках, але якого нема у висновку) символом М, то взаємне розміщення термінів у засновках взятого як приклад силогізму можна відтворити схемою, позначеною нижче символом І. Різних видів розміщення термінів у силогізмі (тобто різних фігур силогізму) є чотири (рис. 6.2):
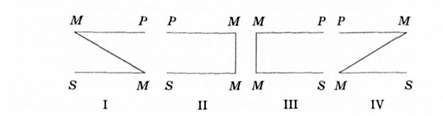
Рис. 6.2. Схематичне зображений фігур силогізму
Структуру силогізму, в якій відтворено вид тверджень, що містяться в ньому, називають модусом силогізму. Скажімо, в прикладі силогізму, наведеному вище, всі три вислови є загальностверджувальними. Оскільки такі твердження у традиційній логіці позначають символом А, то модус силогізму запишемо у вигляді AAA. Модус і фігуру наведеного вище силогізму можна записати в такому разі виразом ААА-1.
Крім загальностверджувальних, силогістика традиційної логіки охоплювала ще три види тверджень: загальнозаперечні (Е), кількісно невизначені (їх часто називають частковими) стверджувальні (І) й заперечні (О). Підставою для таких символів є перша і друга голосні літери у латинських словах ajfirmo (стверджую) і nego (заперечую). Отже, силогізм, у якому два перші твердження (тобто засновки) є загально-стверджувальними, а третій (тобто висновок) - загально-заперечний, записують виразом ААЕ; аналогічно можна записати всі можливі комбінації тверджень у силогізмах.
Різних комбінацій по три символи (два твердження - засновки, третє - висновок) із чотирьох (А, Е, І, О) може бути 64. У такому разі кількість різних за формою силогізмів з урахуванням, що 64 варіанти може бути у кожній з чотирьох фігур, є 256. Із них правильними, тобто такими, у яких за істинності засновків висновок обов'язково є істинним, - усього 24. Ці 24 містять у собі й так звані ослаблені модуси. Модус називають ослабленим, якщо у висновку можна отримати загальне твердження (А або Е), а отримують кількісно невизначене (відповідно, І або О). Неослаблених, тобто сильних, є 19 модусів.
Для полегшення запам'ятовування форм правильних силогізмів у XIII ст. складено вірш (відомі різні його варіанти): Barbara, Celarent, Darii, Ferioque prioris;
Cesare, Camestres, Festino, Baroco secundae;
Tertia Darapti, Disamis, Datisi, Felapton,
Bocardo, Ferison habet; quarta insuper addit
Braman tip, Camenes, Dimaris, Fesaro, Fresison.
У першому рядку перелічено правильні модуси першої (prioris) фігури: у словах Barbara Celarent... голосні літери відтворюють структуру відповідного силогізму (AAA, ААЕ). У наступних рядках наведено правильні модуси другої (secundae), третьої (tertio) і четвертої (quarta) фігур.
Модуси першої фігури Арістотель називав досконалими. Досконалість їх полягає в тому, що для виведення висновку в них достатньо застосувати тільки основну аксіому силогізму, структура якої є узагальненням структури названих модусів першої фігури.
Слова, якими записано структуру модусів, є штучними: основне їх призначення - вміст інформації про операції, якими правильні модуси другої, третьої і четвертої фігур можуть бути перетворені у правильні модуси першої фігури.
Початкова літера у цих словах відповідає початковій літері модусу першої фігури, у який потрібно перетворити цей модус. Наприклад, силогізми, позначені словами Cesare, Camestres, Camenes, потрібно перетворити у другий модус першої фігури.
Літера В в Baroco і Bocardo означає, що потрібно застосувати Barbara для заперечення припущення про неправильність цих модусів. Літера s несе інформацію, що до твердження, позначеного голосною літерою, яка стоїть перед s, потрібно застосувати операцію обернення. Літера m означає, що засновки треба поміняти місцями; літера с, - що виведення повинно полягати у припущенні неправильності модусу. До твердження, позначеного символом, розміщеним перед літерою р, потрібно застосувати обернення з обмеженням, тобто з засновку Усі S є Р отримати висновок Частина Р є S.
Протягом розвитку логіки було сформовано різні методи визначення правильності силогізмів. Один із цих методів, запропонований у середньовіччі, полягає у виявленні відповідності аналізованого силогізму критеріям правильності силогізму. Щоб визначити, чи правильним є силогізм, потрібно перевірити, чи не порушений жоден із критеріїв. Якщо ні, то силогізм правильний, якщо ж хоч одне з правил порушене, то силогізм неправильний.
Правила силогізму:
1. У силогізмі повинно бути тільки три терміни (не більше і не менше).
У силогізмі, наведеному вище, справді є три терміни (люди, ссавці, тварини).
Термін "люди" є суб'єктом висновку, такий термін називають меншим. Термін "тварини" є предикатом висновку, і такий термін називають більшим. Той термін, який міститься в обох засновках і не міститься у висновку, називають середнім терміном.
2. Середній термін повинен бути розподілений принаймні в одному з засновків. Якщо перед терміном, який

Є суб'єктом вислову, стоїть слово всі (тобто й інші варіанти цього логічного терміна - кожен, жоден), то цей термін є розподіленим, в інших випадках суб'єкт твердження нерозподілений. Якщо вислів стверджувальний, то предикат вислову є нерозподіленим, а якщо вислів заперечний, то предикат розподілений. Розподіленість термінів у висловах зафіксовано в таблиці ліворуч.
Зазначене правило стосується крайніх (тобто меншого і більшого) термінів; це терміни, які містяться не тільки у засновках, але й у висновку.
В аналізованому силогізмі перед середнім терміном ссавці у першому засновку є слово всі, отже, друге правило також не порушене.
3. Термін не повинен бути розподіленим у висновку, якщо він не розподілений у засновку. (Якщо перед терміном у засновку не було слова всі, то перед цим терміном у висновку також не повинно бути слова всі. Якщо в засновку термін є предикатом стверджувального вислову, то він не повинен бути предикатом заперечного висновку).
В аналізованому силогізмі це правило не порушене. У засновку перед терміном люди є слово всі, тобто менший термін є розподіленим. Цей термін розподілений також і у висновку, оскільки у висновку перед ним також є слово всі. Термін тварини й у засновку, й у висновку нерозподілений, оскільки в обидвох випадках він є предикатом стверджувального вислову. Отже, третє правило в аналізованому силогізмі також не порушене.
4. Обидва засновки не повинні бути заперечними. В аналізованому силогізмі немає заперечних засновків, отже, це правило в аналізованому силогізмі не порушене.
5. Якщо один зі засновків є заперечним, то і висновок повинен бути заперечним. Оскільки в аналізованому силогізмі немає заперечних засновків, то це правило не є порушеним.
6. Обидва засновки не повинні бути частковими. В аналізованому силогізмі обидва засновки є загальними, отже, це правило не порушене.
7. Якщо один зі засновків є частковим, то і висновок повинен бути частковим. В аналізованому силогізмі нема часткових засновків, отже, це правило також не порушене.
У підсумку отримали, що жодне з семи правил не є порушеним, отже, силогізм правильний.
Зафіксовані вище критерії правильності силогізмів забезпечують коректність оцінки правильності силогізмів тільки в разі строго визначеного тлумачення тверджень, позначених символами А, Е, І, 0. Отже, вони чинні для невеликої кількості тверджень, які насправді використовують люди в своїх міркуваннях. Відношення обсягів, позначувані твердженнями А, Е, І, 0, наведені в табл. 6.1.
Якщо твердженням, що позначувані символами А, Е, І, О, поставити у відповідність інші відношення обсягів, наприклад, якщо твердження А тлумачити як загальностверджувальний невидільний вислів, то, з одного боку, можна підібрати приклади силогізмів, які є правильними згідно з наведеними критеріями правильності, однак насправді вони не є правильними, оскільки з істинних засновків отримуємо хибні висновки. З іншого боку, деякі справді правильні силогізми, відповідно до зазначених критеріїв, будуть оцінені як неправильні.
Таблиця 6.1. Відношення обсягів суб'єкта та предиката у твердженнях, для яких чинні критерії правильності силогізмів

Схожі статті
-
Логіка - Дуцяк І.3. - ЛЕКЦІЯ 3. Виведення знань
3.1. Виведення знань та його види. Алгоритм виявлення правил виведення Отримання одних знань з інших поділяють на два види - виведення і доведення....
-
Логіка - Дуцяк І.3. - ЛЕКЦІЯ 5. Види простих тверджень. Безпосередні виводи
5.1. Види простих тверджень Змістом значної частини тверджень є встановлення відношення між обсягами імен (імена, які містяться в твердженнях, тобто...
-
Логіка - Дуцяк І.3. - ЛЕКЦІЯ 1. Логічні терміни в складних твердженнях
Тема 1. Логічний аналіз складних тверджень ЛЕКЦІЯ 1. Логічні терміни в складних твердженнях 1.1. Прості та складні твердження Для того щоб з'ясувати, що...
-
Логіка - Дуцяк І.3. - 2. Правило для антикон'юнкції
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - 1. Правило для диз'юнкції
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - Правило транзитивності імплікації
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - 6. Правило для еквіваленції
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - 5. Правило для реплікації
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - 4. Правило для імплікації
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - 5.2. Безпосередні виводи
Безпосередніми називають виводи, які містять один засновок. Далі йдеться про виводи, можливість виконання яких зумовлена тим чи іншим відношенням між...
-
Логіка - Дуцяк І.3. - 3. Правило для сильної диз'юнкції
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - 3.3. Відношення логічного випливання та правила виведення
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - Правило контрапозиції
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - 3.2. Найпростіші правила виведення
За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями...
-
Логіка - Дуцяк І.3. - 1.2. Зміст логічних термінів
Тема 1. Логічний аналіз складних тверджень ЛЕКЦІЯ 1. Логічні терміни в складних твердженнях 1.1. Прості та складні твердження Для того щоб з'ясувати, що...
-
Логіка - Дуцяк І.3. - 1.1. Прості та складні твердження
Тема 1. Логічний аналіз складних тверджень ЛЕКЦІЯ 1. Логічні терміни в складних твердженнях 1.1. Прості та складні твердження Для того щоб з'ясувати, що...
-
Логіка - Дуцяк І.3. - 3.1. Виведення знань та його види. Алгоритм виявлення правил виведення
3.1. Виведення знань та його види. Алгоритм виявлення правил виведення Отримання одних знань з інших поділяють на два види - виведення і доведення....
-
Логіка - Дуцяк І.3. - Тема 1. Логічний аналіз складних тверджень
Тема 1. Логічний аналіз складних тверджень ЛЕКЦІЯ 1. Логічні терміни в складних твердженнях 1.1. Прості та складні твердження Для того щоб з'ясувати, що...
-
Логіка - Дуцяк І.3. - Розділ 1. Логічний аналіз тверджень
Тема 1. Логічний аналіз складних тверджень ЛЕКЦІЯ 1. Логічні терміни в складних твердженнях 1.1. Прості та складні твердження Для того щоб з'ясувати, що...
-
Логіка - Дуцяк І.3. - ЛЕКЦІЯ 2. Виявлення несумісності знань
2.1. Види несумісності знань Є різні види несумісності висловів. Один із видів несумісності - несумісність тверджень (логічна хибність тверджень), тобто...
-
Логіка - Дуцяк І.3. - ЛЕКЦІЯ 4. Елементи та структура простих тверджень
ЛЕКЦІЯ 4. Елементи та структура простих тверджень 4.1. Імена. їхні види та властивості Для фіксування знань достатньо двох типів знаків. До них належать...
-
Логіка - Дуцяк І.3. - 5.1. Види простих тверджень
5.1. Види простих тверджень Змістом значної частини тверджень є встановлення відношення між обсягами імен (імена, які містяться в твердженнях, тобто...
-
Логіка - Дуцяк І.3. - Розвиток логіки
Як завершену теоретичну систему, як науку логіку сформував давньогрецький філософ Арістотель. Що таке теоретична система у логіці? Яку теоретичну систему...
-
Логіка - Дуцяк І.3. - 4.3. Структура простих тверджень
Просте твердження - це елементарна послідовність знаків, якою зафіксоване знання. Розповідні речення, мовлені різними мовами, але такі, що мають...
-
Залежно від того, чи мають обсяги імен спільні елементи, між іменами виникають різні відношення (цим відношенням відповідає математичний апарат...
-
Безпосередніми називають виводи, які містять один засновок. Далі йдеться про виводи, можливість виконання яких зумовлена тим чи іншим відношенням між...
-
Логіка - Дуцяк І.3. - 4.2. Відношення між іменами за обсягом (логічні терміни у простому твердженні)
Залежно від того, чи мають обсяги імен спільні елементи, між іменами виникають різні відношення (цим відношенням відповідає математичний апарат...
-
Логіка - Дуцяк І.3. - 2.4. Закони логіки
Інструменти. Алгоритм виявлення суперечності у послідовності пов'язаних тверджень Для виявлення, чи є аналізоване складне твердження суперечливим, треба...
-
Інструменти. Алгоритм виявлення суперечності у послідовності пов'язаних тверджень Для виявлення, чи є аналізоване складне твердження суперечливим, треба...
-
Логіка - Дуцяк І.3. - 2.3. Суперечливі складні твердження
Інструменти. Алгоритм виявлення суперечності у послідовності пов'язаних тверджень Для виявлення, чи є аналізоване складне твердження суперечливим, треба...
Логіка - Дуцяк І.3. - ЛЕКЦІЯ 6. Опосередковані виводи. Силогізми