Страхування - Базилевич В. Д. - 27.6. Визначення мінімально необхідного розміру стартового капіталу страхової компанії

У практичних застосуваннях класичної моделі ризику інтенсивність надходження страхових позовів X та функція розподілу їх величин Р(г) (або ц перші три моменти и2, иА) е параметрами моделі, а відносна страхова надбавка та власний капітал компанії и є змінними, що впливають на міру ризику. На практиці страхові компанії можуть збільшувати або зменшувати розмір параметрів 0 та И Для того, щоб імовірність банкрутства не перевищувала певного безпечного (з погляду компанії) рівня р0. Можна визначити величину стартового капіталу компанії так, щоб ймовірність її банкрутства і|/(и) залишалася на рівні Р0. Коли виплати компанії мають експоненціальний розподіл, рівень стартового капіталу визначається за формулою А

" = -^^1п(р0(1+Є)), (27.46)

Де Р0 - критичний рівень ймовірності банкрутства. Ця формула є оберненою до формули (27.12). Показник мінімального стартового капіталу, розрахований за формулою (27.46), дає змогу кожній страховій компанії визначити, нижче якого рівня небезпечно знижувати обсяг свого власного капіталу (якщо ймовірність банкрутства була нижча за необхідну) або на яку величину треба збільшити розмір власного капіталу чи відносну страхову надбавку (а отже, і загальний обсяг страхових платежів), щоб перебувати на безпечному (з погляду компанії) рівні.

Для того щоб визначити показники мінімального стартового капіталу для забезпечення певного рівня ймовірності банкрутства для обчислених вище шести апроксимацій, необхідно розв'язати рівняння (27.29), (27.34), (27.36), (27.38), (27.39), (27.40) відносно стартового капіталу и.

Так, використовуючи дифузійну апроксимацію, ми отримаємо *

Використовуючи апроксимацію де Вільдера, матимемо

Ц=-1пРо-1п(1+Є)(1+б)А> (27 4g)

Використовуючи експоненціальну апроксимацію, одержимо

-а+1Пр0)Уі4+(4/3)9ц, ц3 + ц2

И= -1 -. (27.49)

2Ці9

Використовуючи апроксимацію Рені, отримаємо:

Ц=Мі+е)іп(рВД+Є))

-2щЄ

Трохи складніше визначити необхідний обсяг стартового капіталу, використовуючи апроксимацію Беекмана - Бовер-са. В цьому випадку вона матиме вигляд

" = ^(1-^(1+6)), (27.61)

Де - функція обернена до гамма-розподілу1 з параметрами рА і а*. Вираз (і-р0(1 + 9)) є аргументом цієї функції. Таку функцію неможливо представити в явному вигляді, проте її значення можна знайти в статистичних таблицях або підрахувати за допомогою засобів програмного пакета Microsoft Excel.

Для апроксимації Лундберга ми не знайдемо розмір стартового капіталу и в явному вигляді, бо він є розв'язком рівняння (27.39), при Ц/І(и) = р0, яке точно в елементарних функціях не розв'язується. Проте за допомогою ітераційних методів розв'язання рівнянь, враховуючи, що функція iy(u), а отже, і її апроксимація vy, (и) є спадними за змінною м, можна з будь-якою заданою точністю визначити необхідний стартовий капітал страхової компанії для забезпечення певного рівня банкрутства.

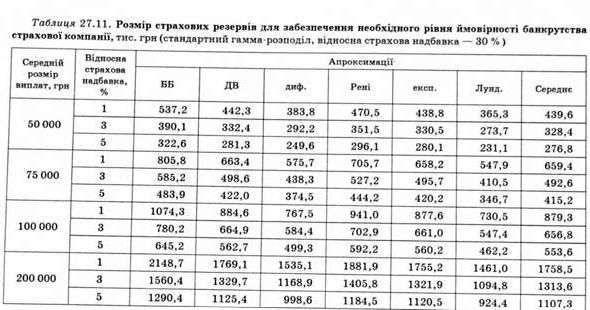
Аналізуючи отримані дані, слід зазначити, що найбільший розмір страхових резервів дає апроксимація Беекмана - Бо-верса, а найменший - апроксимація Лундберга.

Зазначимо, що обчислити мінімальний розмір страхових резервів компанії для будь-якого іншого рівня ймовірності банкрутства, відмінного від наведених у табл. 27.10, 27.11, можна за допомогою електронного аналога цих таблиць у пакеті Microsoft Excel 2002, замінивши у відповідній клітині таблиці значення ймовірності банкрутства.

Таблиця 27.10. Розмір страхових резервів для забезпечення необхідного рівня ймовірності банкрутства страхової компанії, тис. грн (експоненціальний розподіл)

Відносна страхова надбавка

Ймовірність банкрутства,

%

Розмір середніх виплат, грн

60 000

75 000

100 000

200 000

30%

1

940,9

1411,4

1881,9

3763,8

3

702,9

1054,4

1405,8

2811,6

5

592,2

888,3

1184,5

2368,9

40%

1

747,0

1120,5

1494,0

2988,1

3

554,8

832,1

1109,5

2219,1

5

465,4

698,1

930,7

1861,5

50%

1

630,0

944,9

1259,9

2519,8

3

465,2

697,7

930,3

1860,7

5

388,5

582,8

777,1

1554,2

Висновки

1. Динамічна модель банкрутства - одна з основних еконо-міко-математичних моделей страхування.

2. Введено основну характеристику цієї моделі - ймовірність банкрутства страхової компанії.

3. Описано постановку класичної моделі ризику. Сформульовано припущення, необхідні для цієї моделі.

4. Показано, що коли виплати страхової компанії мають експоненціальний розподіл, можна визначити точну формулу для обчислення ймовірності банкрутства.

5. Розглянуто апроксимацію Крамера - Лундберга та характеристичний коефіцієнт.

6. Показано, що на практиці доцільно використовувати наближені оцінки ймовірності банкрутства. Наведено шість таких апроксимацій, здійснено порівняльний аналіз їх точності, показано, що апроксимація де Вільдера у більшості випадків дає найточніший результат.

7. Обчислено точні та наближені оцінки ймовірності банкрутства найбільших страхових компаній України залежно від обсягу їх страхових резервів, відносної страхової надбавки та розміру середніх виплат.

8. Визначено мінімально необхідного розмір стартового капіталу страхової компанії для забезпечення необхідного рівня ймовірності банкрутства.

Навчальний тренінг

Основні терміни і поняття

Динамічна модель банкрутства; класична модель ризику; процес ризику; ймовірність банкрутства; характеристичний коефіцієнт; апроксимація Крамера - Лундберга; нерівність Крамера - Лундберга; апроксимація Беекмана - Боверса; ап-

Роксимація де Вільдора; дифузійна апроксимація; експоненціальна апроксимація; апроксимація Лундберга; апроксимація Рені; мінімальний розмір стартового капіталу.

Схожі статті




Страхування - Базилевич В. Д. - 27.6. Визначення мінімально необхідного розміру стартового капіталу страхової компанії

Предыдущая | Следующая