Менеджмент организаций - Киржнер Л. А. - Задачи, решаемые методами теории массового обслуживания
Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени (поток вызовов на телефонной станции, поток покупателей, поток заявок (требований) на ремонт оборудования и т. п.).
Поток характеризуется интенсивностью - л - частотой появления событий или средним числом событий, поступивших в СМО за единицу времени.
Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.
Поток событий называется потоком без последствий, если для любых двух непересекающихся участков времени τ4 и τ2 - число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие (например, поток пассажиров, входящих в метро, практически не имеет последствий).
Поток событий называется ординарным, если вероятность попадания на малый (элементарный) участок времени ∆t двух или более событий является величиной бесконечно малой по сравнению с вероятностью попадания одного события, т. е. поток требований (событий). Ординарен, если они (события) появляются в нем поодиночке, а не группами.
Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последствий. Название "простейший" объясняется тем, что СМО с простейшими потоками имеет наиболее простое математическое описание.
Математически доказано, что для простейшего потока число т событий (требований), попадающих на произвольный участок времени t распределено по закону Пуассона
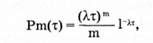
Для которого математическое ожидание случайной величины равно ее дисперсии:
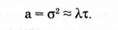
В частности, вероятность того, что за время т не произойдет ни одного события (m = 0), равна
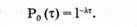
В соответствии с этой формулой вероятность того, что на участке времени длиной t не появится ни одного из последующих событий, равна
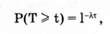
А вероятность противоположного события, т. е. функция распределения случайной величины Т есть
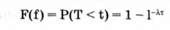
Методы исследования СМО
Процессы массового обслуживания исследуются на основе двух методов:
1. Аналитического.
2. Метода статистического моделирования или метода Монте-Карло.
Каждый из этих методов имеет свои особенности и сферу практического применения.
Аналитическая теория массового обслуживания предлагает достаточно простые расчетные формулы для определения важнейших характеристик функционирования СМО различных классов. Эти подходы изложены в [45].
Однако на практике реальные СМО часто отличаются от упрощенных систем. Обслуживающие аппараты и источники, посылающие требования, заявки могут быть неоднородными. Обслуживание может носить сложный многофазовый характер. Поток событий часто может оказаться не простейшим, а время обслуживания в реальных системах может носить любой характер распределения. Многие самые сложные задачи (особенно возникающие в производственных системах) могут быть успешно решены при помощи метода статистического моделирования случайных процессов (метод Монте-Карло).
Построение математической модели Монте-Карло состоит из следующих этапов:
1. Формирование целей задачи и выбор ограничительных условий функционирования системы обслуживания.
2. Проведение наблюдений за ходом производства, т. е. получение исходных данных.
3. Первичная обработка данных, построение рядов распределения и их графический анализ. Выдвижение гипотезы о характере закона распределения.
4. Построение теоретического распределения с параметрами данных эмпирического наблюдения.
5. Проверка соответствия теоретического и эмпирического распределения.
Для наблюдения заходом производственного процесса используются данные фотографий, хронометража, журналов регистрации простоев оборудования, данные с АИС (автоматизированных информационных систем) и др. методы получения информации. При проведении наблюдений не следует проводить округления до равных значений времени.
При обработке первичной документации важно правильно выбрать интервалы группировок. Если ожидается, что распределение похоже на нормальное, величина интервала рассчитывается по формуле:
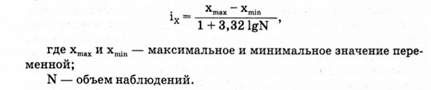
Рассмотрим, как происходит поиск этой кривой. Вначале собираются исходные данные, строится гистограмма и определяют закон распределения. Далее строится теоретическая кривая, параметры которой совпадают с параметрами эмпирического распределения. Для этого необходимо найти параметры эмпирического распределения и по ним построить теоретическую кривую. Выдвинуть форму гипотезы, найти параметры и построить кривую и далее проверить, насколько соответствует теоретическая кривая и эмпирическое распределение. Если они полностью совпадают, то, значит, закон найден. Но если между теоретической кривой и эмпирической гистограммой имеются различия, необходимо проверить на сколько существенны эти различия. Если они носят случайный характер, тогда можно считать, что эмпирическое распределение описывается данной теоретической кривой. Если же различия очень велики, значит, теоретический закон подобран в данном случае неверно, и нужно искать новый закон распределения. Для оценки существенности различий теоретической кривой и эмпирического распределения используется два критерия X2 (х-квадрат) Пирсона и λ лямбда Колмогорова. X2 определяется по следующей формуле:
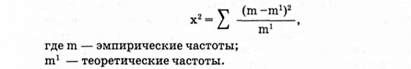
Теоретические частоты находятся на основе, например, интегральной формы распределения путем умножения на объем совокупности.
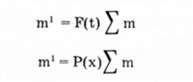
В результате получаем теоретически накопленные частоты.
Оценка на основе критерия х2 производится следующим образом. После того, как найдено х определяют число степеней свободы К, которое равно числу интервалов минус число статистических характеристик, использованных при расчете распределения (параметров). При нормальном законе - три (x,σ,N) параметра, а при распределении Пуассона - два (λ и N) параметра. Для полученных величин X2 и числа степеней свободы К по таблицам отыскивается вероятность Рх2 того, что различие между теоретическим и эмпирическим распределениями носит случайный характер. Если Рх2 больше 0,05 или 5%, можно считать, что эта вероятность достаточно велика, чтобы не исключать случайного характера различий и поэтому распределение считают подчиняющимся данному теоретическому закону. Если же Рх2 меньше 5 %, то считается, что теоретическое и эмпирическое распределение не совпадают и тогда нужно искать новое теоретическое распределение. Значения Рх2 содержатся в специальных таблицах с двумя входами: один соответствует х2, второй - К. На их пересечении Рх2. Проверка по критерию λ. производится так: вначале определяют
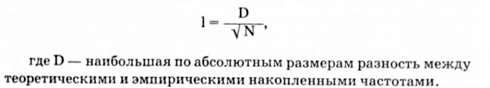
После того, как найдена А, по таблицам находят Р (λ). И, если оно больше 0,05, считают, что различия распределения носят случайный характер, если меньше, то не случайный. Критерий λ по сравнению х2 являются менее жестким, т. е. обычно он показывает большую вероятность того, что различие между распределениями носит случайный характер. Это объясняется тем, что для использования критерия λ нужно дополнительное условие, а именно, теоретический анализ должен показать, что эмпирическое распределение должно подчиняться данному закону.
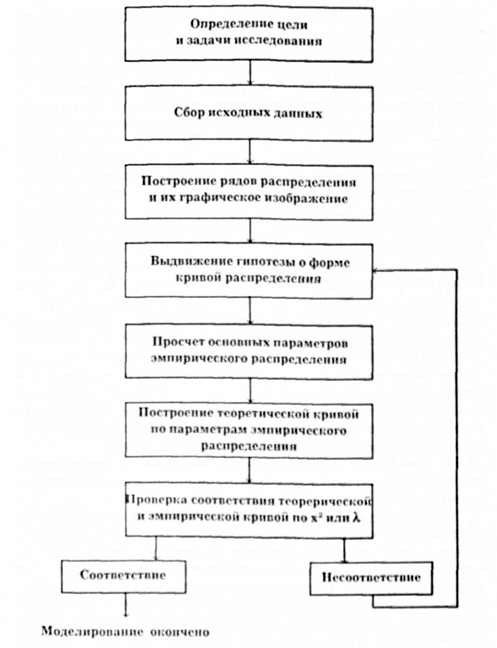
Рис.6.3.
После того как построена математическая модель производственного процесса, можно переходить к проведению случайных испытаний и моделированию на их основе хода производственного процесса. Случайные испытания производятся обычно на основе равновероятного распределения. Далее необходимо от равновероятного распределения перейти к распределению, которое описывается математической моделью. Наконец, построение графика Эпроизводственного процесса на основе случайных испытаний. Для проведения случайных испытаний используются различные методы. Теоретически наиболее простой, но практически наиболее трудоемкий метод жеребьевки: случайный отбор по схеме повторного отбора (шары из урны), моделирование случайных испытаний с помощью ЭВМ, использование таблиц случайных чисел, составленных на основе одного из первых двух способов. Пользоваться таблицей можно в любом, но заранее оговоренным порядке (или по диагонали, сверху вниз и т. д.).
Преобразование равновероятных случайных чисел в числа, подчиняющиеся установленному ранее закону распределения
Имеется несколько переходов от нормально распределенных чисел к случайным числам.
Первый способ связан с закреплением за каждым значением определенного количества номеров, оно пропорционально вероятности каждого времени (например, телефонный разговор).
Этот способ хорош для дискретных значений. Если же значения непрерывные, то используем функцию нормального распределения.
Поскольку вероятность любого значения от 0 до 1, т. е. 0 ≤ F(t) < 1, может быть рассчитано с любой точностью до 2, 3 и т. д. знаков. Найдя по таблице случайных чисел значения случайных чисел, можно приравнять их к величинам F(t)t и известным значениям x и σ значения χ. Эти значения χ и представляют собой случайные величины промежутков между обслуживанием или длительность обслуживания, подчиняющимся закону нормального распределения С параметрами σ и χ. Такой метод очень трудоемкий, и поэтому на практике употребляется графический метод как наиболее удобный.
Установив на основе случайных испытаний возможные длительности времени обслуживания, либо длительности промежутков между поступлением заявок, строят график движения процесса производства во времени. На таком графике проставляют время работы оборудования и время обслуживания, простои и ожидания обслуживания. Суммирование времени простоев дает возможность оценить затем каждый вариант с точки зрения уровня обслуживания основного производственного процесса. Эта оценка представляет третью стадию решения задачи, а именно: оценку и анализ результатов моделирования. В ходе такой оценки строится график экономичности различных вариантов обслуживания. При оценке учитывают, что:
1. Потери и затраты состоят из затрат на обслуживание (зарплата наладчиков) и потерь, связанных с простоями.
2. Экономически наибольшую сложность представляет определение потерь от простоев.
3. Важно установить, сколько нужно произвести испытаний, чтобы определить норму обслуживания. Жесткой цифры нет.
Для определения того, достаточно ли проведено испытаний, используется следующий прием. Общее количество испытаний делится на две части. Для каждой половины подсчитывается средняя арифметическая и дисперсия. Далее они сравниваются друг с другом. Оценка расхождения между средними производится по критерию Стьюдента
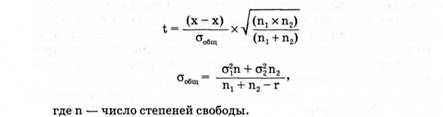
Затем сравниваем tрасч с табличным значением. Если tрасч больше табличного, значит, расхождения между средними велики. Это говорит о том, что испытаний в таком случае недостаточно. Испытания продолжают и затем делают снова проверку.
Величина t находится по таблицам Стьюдента в зависимости от вероятности возможной ошибки. Обычно в пределах 5 % и от числа степеней свободы.
Задачи, решаемые методами теории массового обслуживания
Расчет численности вспомогательных рабочих (расчет норм обслуживания): наладчиков, электриков, дежурных слесарей. Расчет необходимого числа кранов. Определение страховых заделов. Определение страховых запасов. Расчет необходимой площади материальных складов.
Схожі статті
-
Менеджмент организаций - Киржнер Л. А. - Методы исследования СМО
Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени (поток вызовов на...
-
Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени (поток вызовов на...
-
Менеджмент организаций - Киржнер Л. А. - Потоки событий (требований)
Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени (поток вызовов на...
-
Менеджмент организаций - Киржнер Л. А. - Классификация систем массового обслуживания
В практике человеческой деятельности большое место занимают процессы массового обслуживания, которые возникают в системах, предназначенных для...
-
Менеджмент организаций - Киржнер Л. А. - 6.5. Модели массового обслуживания
В практике человеческой деятельности большое место занимают процессы массового обслуживания, которые возникают в системах, предназначенных для...
-
Менеджмент организаций - Киржнер Л. А. - Современные теории постановки целей
Постановка целей имеет традиции, которые начались с управления по заданию, продолжались в целевом управлении вплоть до современного стратегического...
-
Менеджмент организаций - Киржнер Л. А. - 6. МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
6.1. Сущность моделирования. Классификация моделей Одним из исследовательских видов человеческой деятельности является моделирование, т. е. способ...
-
5.1. Природа и содержание процесса принятия решений Принятие решений является важнейшей частью управленческой деятельности. Незаметные на первый взгляд...
-
Менеджмент организаций - Киржнер Л. А. - 4.2. Характеристика целей и их установление
Миссия задает общие ориентиры направления функционирования организации; конкретные конечные состояния, к которым стремится организация, фиксируются в...
-
Менеджмент организаций - Киржнер Л. А. - Стадии и этапы принятия рационального решения
На процесс принятия решений влияют три основных фактора: чувства, опыт, знания. В зависимости от преобладающего влияния одного из них выделяют...
-
Менеджмент организаций - Киржнер Л. А. - 5.3. Выработка и принятие управленческих решений
На процесс принятия решений влияют три основных фактора: чувства, опыт, знания. В зависимости от преобладающего влияния одного из них выделяют...
-
Менеджмент организаций - Киржнер Л. А. - 5.2. Классификация управленческих решений
В связи с деятельностью организации, направленной на достижение своих целей, возникает множество проблем, т. е. сложных теоретических или практических...
-
Менеджмент организаций - Киржнер Л. А. - 5.1. Природа и содержание процесса принятия решений
5.1. Природа и содержание процесса принятия решений Принятие решений является важнейшей частью управленческой деятельности. Незаметные на первый взгляд...
-
Менеджмент организаций - Киржнер Л. А. - Постановка целей и обратная связь
Постановка целей имеет традиции, которые начались с управления по заданию, продолжались в целевом управлении вплоть до современного стратегического...
-
1. ОРГАНИЗАЦИЯ КАК ОБЪЕКТ УПРАВЛЕНИЯ, ВЗАИМОСВЯЗЬ И ВЗАИМОЗАВИСИМОСТЬ ЕЕ ВНУТРЕННИХ ЭЛЕМЕНТОВ И ФАКТОРОВ ВНЕШНЕЙ СРЕДЫ 1.1. Природа организаций....
-
Менеджмент организаций - Киржнер Л. А. - Характер собственности
По данному признаку различают следующие виды фирм: частные, государственные, кооперативные. Частные фирмы могут существовать в виде самостоятельных...
-
1. ОРГАНИЗАЦИЯ КАК ОБЪЕКТ УПРАВЛЕНИЯ, ВЗАИМОСВЯЗЬ И ВЗАИМОЗАВИСИМОСТЬ ЕЕ ВНУТРЕННИХ ЭЛЕМЕНТОВ И ФАКТОРОВ ВНЕШНЕЙ СРЕДЫ 1.1. Природа организаций....
-
Менеджмент организаций - Киржнер Л. А. - 2.2. Основные функции управления
Функция (лат. fundio - исполнение, осуществление). Сущность любого явления выражается в его функциях, т. е. тех задачах, для решения которых оно...
-
Менеджмент организаций - Киржнер Л. А. - 2.1. Принципы управления промышленным предприятием
2.1. Принципы управления промышленным предприятием Принцип (от лат. principium - начало, основа) - основное, исходное положение для осуществления...
-
Менеджмент организаций - Киржнер Л. А. - 2. ОСНОВНЫЕ ПРИНЦИПЫ И ФУНКЦИИ УПРАВЛЕНИЯ ОРГАНИЗАЦИЕЙ
2.1. Принципы управления промышленным предприятием Принцип (от лат. principium - начало, основа) - основное, исходное положение для осуществления...
-
Менеджмент организаций - Киржнер Л. А. - Принадлежность капитала и контроль
По этому признаку различают следующие виды фирм: национальные, иностранные, смешанные, совместные. Национальные - фирмы, капитал которых принадлежит...
-
Менеджмент организаций - Киржнер Л. А. - Построение модели оптимального планирования
Решение практических задач связано с тремя основными этапами исследования: составление экономико-математической модели, определение оптимального решения...
-
Менеджмент организаций - Киржнер Л. А. - 6.4. Модели оптимального планирования
Особенность экономико-математических моделей оптимизации состоит в том, что они основаны на строгих теоретических положениях математического...
-
Менеджмент организаций - Киржнер Л. А. - 6.3. Модели управления запасами
Для осуществления нормальной деятельности фирмы создаются запасы (резервы). Правильное и своевременное определение оптимальной стратегии управления...
-
Менеджмент организаций - Киржнер Л. А. - 6.1. Сущность моделирования. Классификация моделей
6.1. Сущность моделирования. Классификация моделей Одним из исследовательских видов человеческой деятельности является моделирование, т. е. способ...
-
Менеджмент организаций - Киржнер Л. А. - Руководители низового уровня
Работа младших начальников координируется я контролируется руководителями среднего звена. В большой организации может быть столько руководителей среднего...
-
Менеджмент организаций - Киржнер Л. А. - 5.4. Применение к разработке решений научных подходов
Эффективность управленческого решения определяется обоснованностью методологии решения проблем, подходов, принципов, методов. Анализ теории и практики...
-
Менеджмент организаций - Киржнер Л. А. - Руководители среднего звена
Работа младших начальников координируется я контролируется руководителями среднего звена. В большой организации может быть столько руководителей среднего...
-
Менеджмент организаций - Киржнер Л. А. - Организация, ориентированная на рынок
Данный тип организации является на практике своего рода комбинацией вышерассмотренных новых типов. По характеру взаимодействия с внешней средой, то есть...
-
Менеджмент организаций - Киржнер Л. А. - 3.2. Типы организаций по взаимодействию с человеком
Различие между организациями зависит от характера взаимодействия между индивидом и организацией в целом. Основой данного различия является разница в...
Менеджмент организаций - Киржнер Л. А. - Задачи, решаемые методами теории массового обслуживания