Логіка - Мозгова Н. Г. - 6. Протиставлення предикатові
Перетворення - це логічна операція, в результаті якої судження змінює свою якість, а предикат висновку заперечує предикат засновку. Кількість судження при цьому не змінюється.
У залежності від чотирьох типів простих категоричних суджень існують такі правила перетворення суджень.
Загальностверджувальне судження.
А(8Р) -> Е(8 - Р): "Усі 8 є Р, отже, жодне 8 не є не Р".
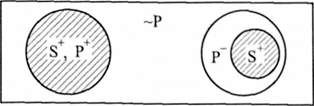
Основою утворення умовиводу тут виступає закономірність відношення обсягів двох суперечливих понять, які є предикатами одного і
Того самого суб'єкта. Відомо, що два суперечливих поняття (Р і ~Р) завжди вичерпують обсяг свого родового поняття. Якщо відомо, що даний предмет входить до обсягу Р, то це є підставою для висновку, що він не входить до обсягу ~Р, і навпаки. Подвійне заперечення (не є не Р), що використовується у судженні-висновку означає рівнозначність цих двох суджень.
Наприклад:
А Усі адвокати - юристи.
Е Жоден адвокат не є не юристом.
Загальнозаперечне судження.
E(SP) -> A(S ~Р): "Жодне S не є Р, отже, всі S є не Р".
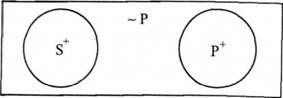
Наприклад:
Жодна кішка не є собакою. Усі кішки є не собаками.
Частковостверджувальне судження.
1(SP) -"0(S ~Р): "Деякі S є Р, отже, деякі S не є не Р".
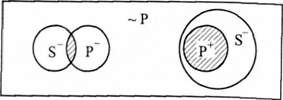
Наприклад:
Деякі студенти є відмінниками. Деякі студенти не є не відмінниками.
Частковозаперечне судження.
О(БР) -> 1(5 ~Р): "Деякі Б не є Р, отже, деякі Б є не Р".
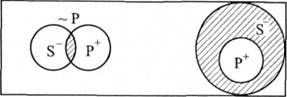
Наприклад:
Деякі жінки не є депутатами. Деякі жінки є не депутатами.
6. Протиставлення предикатові
Протиставлення предикатові - це логічна операція, яка складається з двох попередніх, тобто: 1) судження змінює якість на протилежну, а в деяких випадках змінюється і кількість судження; 2) Б та Р судження-висновку міняються місцями; 3) Р висновку є поняттям, заперечним (~Р) до Р засновку.
У залежності від чотирьох типів простих категоричних суджень існують такі правила протиставлення предикатові.
Загальностверджувальне судження.
А(8Р) -" Е(~ РБ): "Усі 8 є Р, отже, жодне не Р не є 5".
Наприклад:
Усі правильні трикутники є рівнобічними. Жоден нерівнобічний трикутник не є правильним.
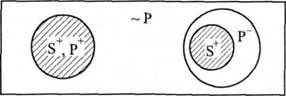
Загальнозаперечне судження.
E(SP) -> I(~PS): "Жодне S не є Р, деякі не Р є S".
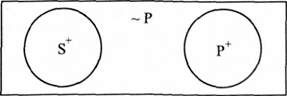
Наприклад:
Жоден кит не є рибою. Деякі не риби є китами.
Оскільки, в поняття "не риби" включається багато видів тварин (крім китів), то ми кажемо "деякі", але не "всі". Частковозаперечне судження. 0(8Р) -"І(~Р8): "Деякі 8 не є Р, отже, деякі не Р є 8 ".
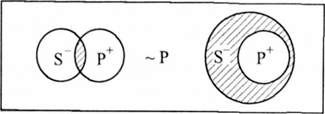
Наприклад:
Деякі злочинці не є повнолітніми. Деякі неповнолітні є злочинцями.
Частковостверджувальне судження не завжди дає необхідні виводи при протиставленні предикатові, тобто висновки з протиставлення предикатові судження І(8Р) не завжди є істинними (а часто навіть позбавлені здорового глузду). Наприклад: "Деякі люди є вегетаріанцями, отже, деякі невегетаріанці не є людьми (?!)". Виходячи з цього, частково-стверджувальне судження протиставленню предикатові не підлягає.
7. Виводи за логічним квадратом
Знаючи типи та характер відношень простих категоричних суджень за значенням їх істинності, можна робити достовірні умовиводи з будь-якого категоричного судження.
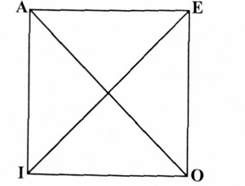
Нагадаємо, що за логічним квадратом існують такі типи відношень між категоричними судженнями:
1) Відношення протилежності (А - Е) - ці судження не можуть бути одночасно істинними.
2) Відношення часткової сумісності (І - О) - вони не можуть бути одночасно хибними.
3) Відношення підпорядкування (А - І, Е - О) - якщо загальне судження істинне (А, Е), то часткове (І, О) не може бути хибним. Інакше це відношення називають відношенням логічного слідування.
4) Відношення суперечності (А - О, Е -1) - якщо одне з них істинне, то інше (суперечливе) необхідно хибне, і навпаки.
Для того, щоб зробити умовиводи за логічним квадратом, необхідно:
1) Визначити тип судження-засновку та значення його істинності.
2) Сформулювати три інші типи суджень з тими ж самими 8 та Р та визначити значення істинності отриманих суджень-висновків.
3) Перевірити відповідність їх значень істинності при встановленні чотирьох типів відношень між судженнями.
Наприклад:
1) Судження-засновок: "Усі студенти-юристи вивчають логіку" - А(8Р), істинне.
2) Е(8Р) - "Жоден студент-юрист не вивчає логіку" - хибне; І(8Р) - "Деякі студенти-юристи вивчають логіку" - істинне; 0(8Р) - "Деякі студенти-юристи не вивчають логіку" - хибне.
Подивимось на відношення:
A) протилежність - А (істина) - Е (хиба);
B) часткова сумісність - І (істина) - О (хиба);
C) підпорядкування - А (істина) - І (істина), Е (хиба) - О (хиба); сі) суперечність - А (істина) - О (хиба), Е (хиба) -1 (істина). Оскільки значення істинності цих пар суджень відповідає визначенням логічних відношень між ними, то виводи зроблено правильно.
Література для поглибленого вивчення розділу
A. Основна.
1. Гетманова А. Д. Логика. - М.: Новая школа, 1995.-С. 121-136.
2. ЖеребкінВ. Є. Логіка.-X.:Основа;К.:Знання, 1999.-С. 108-134.
3. Кириллов В. И., Старченко А. А. Логика. - М.: Высшая школа, 1995. - С. 120-143.
4. Конверський А. Є. Логіка. - К.: Четверта хвиля, 1998. - С. 228-239.
5. Иванов Е. А. Логика. - М.: Издательство БЕК, 1996. - С. 173-200.
6. Свинцов В. И. Логика.-М.: Скорина; Весь мир, 1998.-С. 203-231.
7. Тофтул М. Г. Логіка: Навч. посібн. для студентів вищих навчальних закладів. - К.: Академія, 2003. - С. 162-169.
8. Хоменко І. В.,АлексюкІ. А. Основи логіки.-К.: Золоті ворота, 1996. - С. 96-145.
9. Хоменко І. В. Логіка: Підручник для студентів вищих навчальних закладів. - К.: Абрис, 2004. - С. 143-148.
B. Додаткова.
1. Ивин А. А. Искусство правильно мыслить. - М.: Просвещение, 1990. - С. 6-57.
2. Кондаков Н. И. Логический словарь-справочник. - М: Наука, 1975. - Статті: выведение, дедукция, непосредственное умозаключение, обращение, превращение, противопоставление предикату, умозаключение, энтимема, эпихейрема та інші статті до даної теми.
3. Логические методы и формы научного познания. - К.: Наукова думка, 1984.-200 с.
4. Мельников В. Н. Логические задачи. - К.; Одесса: Вища школа, 1989. - С. 292-314.
5. Шейко О. М. Скорочений силогізм. - К.: Вища школа, 1962. - 28 с.
Схожі статті
-
Логіка - Мозгова Н. Г. - 5. Перетворення судження
Перетворення - це логічна операція, в результаті якої судження змінює свою якість, а предикат висновку заперечує предикат засновку. Кількість судження...
-
Логіка - Мозгова Н. Г. - 2. Відношення еквівалентності
Короткий зміст розділу Судження відображають зв'язки і відношення між предметами об'єктивної дійсності. Якщо судження правильно відображають предмети...
-
Логіка - Мозгова Н. Г. - 1. Поняття про логічні відношення між простими судженнями
Короткий зміст розділу Судження відображають зв'язки і відношення між предметами об'єктивної дійсності. Якщо судження правильно відображають предмети...
-
Логіка - Мозгова Н. Г. - 4. Обернення судження
Умовами здобуття істинних висновків в умовиводі є: 1) істинність вихідних висловлювань або засновків; 2) правильність виводу. Поняття істинного...
-
Логіка - Мозгова Н. Г. - 3. Правильний та неправильний умовивід
Умовами здобуття істинних висновків в умовиводі є: 1) істинність вихідних висловлювань або засновків; 2) правильність виводу. Поняття істинного...
-
Короткий зміст розділу Судження відображають зв'язки і відношення між предметами об'єктивної дійсності. Якщо судження правильно відображають предмети...
-
Логіка - Мозгова Н. Г. - 3. Закон тотожності
*Закон тотожності як закон правильного мислення є певною формою відображення закону об'єктивної дійсності - визначеності, певної відносної сталості...
-
Логіка - Мозгова Н. Г. - 6. Виділяюче судження
Дещо стверджувати або заперечувати можна стосовно одного предмета, частини предметів та всіх предметів деякої множини предметів. У залежності від цього...
-
Логіка - Мозгова Н. Г. - 7. Відношення суперечності. Закон виключеного третього
Нагадаємо, що несумісними є судження, які не бувають одночасно істинними. Першим видом несумісності є протилежність (контрарність). У відношенні...
-
Логіка - Мозгова Н. Г. - 6. Відношення протилежності. Закон суперечності
Нагадаємо, що несумісними є судження, які не бувають одночасно істинними. Першим видом несумісності є протилежність (контрарність). У відношенні...
-
Логіка - Мозгова Н. Г. - 5. Відношення підпорядкування
*Закон тотожності як закон правильного мислення є певною формою відображення закону об'єктивної дійсності - визначеності, певної відносної сталості...
-
Логіка - Мозгова Н. Г. - 4. Відношення часткової сумісності
*Закон тотожності як закон правильного мислення є певною формою відображення закону об'єктивної дійсності - визначеності, певної відносної сталості...
-
Логіка - Мозгова Н. Г. - 5. Поділ простих суджень за кількістю
Дещо стверджувати або заперечувати можна стосовно одного предмета, частини предметів та всіх предметів деякої множини предметів. У залежності від цього...
-
Логіка - Мозгова Н. Г. - 8. Розподіленість термінів у категоричних судженнях
Оскільки кожне судження одночасно має якісну і кількісну характеристику, то буде доцільним об'єднати два попередніх поділи суджень за якістю і кількістю....
-
Оскільки кожне судження одночасно має якісну і кількісну характеристику, то буде доцільним об'єднати два попередніх поділи суджень за якістю і кількістю....
-
Логіка - Мозгова Н. Г. - 2. Види умовиводів
Розділ 7. Безпосередній дедуктивний умовивід Короткий зміст розділу Знання людини про навколишній світ поділяються на безпосередні та опосередковані....
-
Логіка - Мозгова Н. Г. - 1. Поняття умовиводу та його структура
Розділ 7. Безпосередній дедуктивний умовивід Короткий зміст розділу Знання людини про навколишній світ поділяються на безпосередні та опосередковані....
-
Логіка - Мозгова Н. Г. - Розділ 7. Безпосередній дедуктивний умовивід
Розділ 7. Безпосередній дедуктивний умовивід Короткий зміст розділу Знання людини про навколишній світ поділяються на безпосередні та опосередковані....
-
Логіка - Мозгова Н. Г. - МОДУЛЬ 3. УМОВИВІД
Розділ 7. Безпосередній дедуктивний умовивід Короткий зміст розділу Знання людини про навколишній світ поділяються на безпосередні та опосередковані....
-
Логіка - Мозгова Н. Г. - 5. Відношення логічного слідування
Серед формул логіки висловлювань є такі, які незалежно від значень істинності їх атомів є завжди істинними. їх називають тотожно істинними формулами або...
-
Логіка - Мозгова Н. Г. - 4. Особливості імплікації
Серед формул логіки висловлювань є такі, які незалежно від значень істинності їх атомів є завжди істинними. їх називають тотожно істинними формулами або...
-
Логіка - Мозгова Н. Г. - 3. Відношення еквівалентності між складними висловлюваннями
Серед формул логіки висловлювань є такі, які незалежно від значень істинності їх атомів є завжди істинними. їх називають тотожно істинними формулами або...
-
Логіка - Мозгова Н. Г. - 4. Поділ простих суджень за якістю
Усі судження поділяються на прості та складні. Простим називають судження, яке виражає зв'язок двох і тільки двох понять. Судження, яке складається з...
-
Логіка - Мозгова Н. Г. - 3. Прості судження, їх види та структура
Усі судження поділяються на прості та складні. Простим називають судження, яке виражає зв'язок двох і тільки двох понять. Судження, яке складається з...
-
Логіка - Мозгова Н. Г. - 8. Відношення між поняттями
Поділ понять за обсягом ілюструє наведена схема. Загальні поняття відображають ознаки певної множини предметів, наприклад, "село", "місто", "людина",...
-
Логіка - Мозгова Н. Г. - 7. Види понять за змістом
Поділ понять за обсягом ілюструє наведена схема. Загальні поняття відображають ознаки певної множини предметів, наприклад, "село", "місто", "людина",...
-
Логіка - Мозгова Н. Г. - 6. Поділ поняття та його види
При вивченні деякого поняття перед нами часто виникає питання про необхідність розкриття його обсягу, тобто розподілу предметів, які містяться в понятті,...
-
Логіка - Мозгова Н. Г. - 5. Неявні визначення та прийоми, подібні до визначення
Визначення повинно бути не тільки істинним за змістом, але й правильним за своєю структурою. Правильність визначення залежить від дотримання певних...
-
Логіка - Мозгова Н. Г. - Розділ 6. Складне судження
Короткий зміст розділу Складне судження (висловлювання) є об'єктом вивчення розділу логіки, який називають *логікою висловлювань. Логіка висловлювань є...
-
Логіка - Мозгова Н. Г. - 4. Правила визначення поняття
Визначення повинно бути не тільки істинним за змістом, але й правильним за своєю структурою. Правильність визначення залежить від дотримання певних...
Логіка - Мозгова Н. Г. - 6. Протиставлення предикатові