Логіка - Мозгова Н. Г. - 1. Поняття та структура доведення

Короткий зміст розділу

Особливістю наукового пізнання є те, що нові результати визнаються істинними і включаються в основи окремої науки, якщо вони пройшли логічну перевірку на обгрунтованість і вважаються доведеними. Ці вимоги стосуються й інших сфер людської діяльності, де є потреба в обгрунтуванні істинності будь-яких тверджень (суджень). Логічний механізм обгрунтування істинності висловлювань вивчається розділом логіки, який називають теорією доведення, або аргументації.

1. Поняття та структура доведення

Доведення - це логічна операція обгрунтування істинності будь-якого судження за допомогою інших істинних і пов'язаних з ним суджень.

Логіка вивчає операцію доведення, відволікаючись від конкретного змісту думок. У структурі доведення розрізняють тезу, аргументи та демонстрацію.

*Теза доведення - це судження (твердження), істинність якого обгрунтовують у процесі доведення. Тезою доведення можуть бути теоретичні твердження науки, узагальнення емпіричних фактів, судження про властивості чи причини виникнення окремих предметів або подій тощо.

* Аргументи - це вихідні теоретичні або фактичні твердження, за допомогою яких обгрунтовується теза. Аргументами можуть бути: знання про окремі події (факти), теорії, аксіоми, постулати, визначення тощо, тобто твердження, істинність яких вважається безумовною.

Демонстрація, або аргументація - це логічний зв'язок між аргументами та тезою. Аргументи як достатні підстави для тези знаходяться з тезою у відношенні логічного слідування:

Це означає, що за умови істинності аргументів, теза теж буде завжди істинною. Таким чином, логічний перехід від аргументів до тези відбувається в формі умовиводу. Це, як правило, ланцюжок розмірковувань або умовиводів, засновками в якому є аргументи, а висновкам - теза. Продемонструвати - значить показати, що теза логічно слідує з допущених аргументів за правилами відповідних умовиводів.

Отже, в процесі доведення для деякого висновку (тези) відновлюють засновки виводу (аргументи).

Обгрунтування тези може відбуватись у формі дедуктивних умовиводів, індукції та аналогії. Ми будемо розглядати тільки дедуктивне доведення.

2. Правила формально-логічного доведення

Правилом доведення є будь-яка правильна структура виводу* тобто така формула, в якій між засновками та висновком існує відношення логічного слідування. Ясно, що формула логіки висловлювань, яка відображає правильну структуру виводу, є завжди істинною формулою або законом логіки.

*Основними правилами доведення (виводу) є такі:

1. Правило введення кон'юнкції (ВК):

А. В-з двох істинних суджень логічно слідує їх кон'юнкція. Якщо істинність двох А Л В тверджень є доведеною, то можна утворити їх кон'юнкцію і використовувати як новий аргумент.

2. Правило введення диз'юнкції (ВД):

А. В - з істинного судження логічно слідує диз'юнкція його з будь-яким А V В, А V В та іншим судженням. Якщо істинність деякого твердження є доведеною, то можна утворити нове твердження-аргумент - диз'юнкцію даного з будь-яким іншим, оскільки диз'юнкція буде істинною при істинності принаймні одного з них - А або В.

3. Правило усунення кон'юнкції (УК):

А Л В. АЛВ - з істинної кон'юнкції логічно слідує висловлювання, що є одним з її А В членів. Якщо істинність кон'юнкції є доведеною, то можна відокремити один з її членів і використовувати як новий аргумент.

4. Правило усунення диз'юнкції (УД), або правило modus tollendo ponens (mtp):

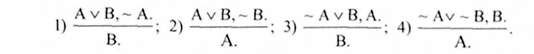
З диз'юнкції двох висловлювань і заперечення одного з них логічно випливає друге висловлювання. Якщо є істинна диз'юнкція і доведено хибність одного з цих тверджень, то можна вважати друге висловлювання істинним і використовувати його як самостійний аргумент.

5. Правило modus ponens (mр):

З істинної імплікації та формули, що є її антецедентом, логічно слідує формула-консеквент цієї імплікації. Якщо умовне висловлювання та його підстава є достовірними, то можна відокремити формулу-наслідок цієї імплікації і використовувати як самостійний аргумент. Це правило ще називають відокремленням консеквента (наслідку).

6. Правило modus tollens (mt):

З істинної імплікації та формули, що є запереченням її консеквента, логічно слідує формула-заперечення її антецедента. Якщо істинність умовного судження та заперечення його наслідку є доведеними, то можна відокремити формулу-заперечення підстави цього судження і використовувати її як самостійний аргумент.

Крім цих основних правил виводу у формальному доведенні можна використовувати й інші правильні структури виводу або закони логіки.

Схожі статті




Логіка - Мозгова Н. Г. - 1. Поняття та структура доведення

Предыдущая | Следующая