Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 12.4. Розв'язування матричних ігор розміру 2x2
Якщо матрична гра не має сідлової точки, то використання чистих стратегій не дає оптимального рішення гри. Так матрична гра, яку розглянуто у прикладі 12.3, не має сідлової точки. В цьому випадку можна отримати оптимальне рішення, випадково обираючи чисті стратегії.
Якщо матрична гра не має сідлової точки, то виникає необхідність гри в змішаних стратегіях.

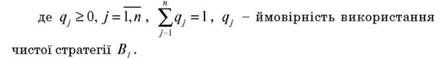
Змішані стратегії представлять математичну модель мінливої і гнучкої тактики гравця, при якій його противник не може довідатись заздалегідь про те становище, в якому йому доведеться опинитись. Перед кожною партією відбувається випадковий вибір однієї з чистих стратегій з деякою певною і вже визначеною ймовірністю.
Гравці вибирають стратегії випадково і незалежно один від одного, тому гра має випадковий характер і сума виграшу теж стає випадковою.
За принципом мінімаксу (максиміну) визначається оптимальне рішення гри - це пара оптимальних стратегій SoA, SoB в загальному випадку змішаних, які мають властивість: якщо один з гравців дотримується своєї оптимальної стратегії, то другому не може бути вигідно відступати від своєї оптимальної стратегії.
Виграш, що відповідає оптимальному рішенню гри, називається ціною гри.
Ціна гри - це об'єктивно можливий середній виграш
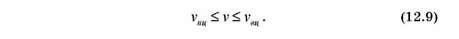
Основна теорема теорії ігор - теорема Неймана: кожна скінченна гра має хоча б одне оптимальне рішення, можливо серед змішаних стратегій.
Якщо чиста стратегія входить в оптимальну з певною ймовірністю, яка відрізняється від нуля, то вона називається активною стратегією.
Теорема про активні стратегії: якщо один із гравців дотримується своєї оптимальної змішаної стратегії, то його виграш залишиться незмінним і буде дорівнювати ціні гри, якщо другий гравець не вийде за границі своїх активних стратегій.
Зміст теореми полягає в тому, що при послідовному дотриманні одним з гравців оптимальної змішаної стратегії, то його виграш не менше ціни гри, незалежно від дій другого гравця, який не вимозі змінити результат гри.
12.4. Розв'язування матричних ігор розміру 2x2
Розглянемо матричну парну гру розміру 2x2.
Таблиця 12.9. Матрична парна гра розміру 2x2

Якщо така гра має сідлову точку, то оптимальне рішення - це пара чистих стратегій, які відповідають цій точці.
Якщо матрична гра не має сідлової точки, то основною теоремою теорії ігор вона має хоча б одне оптимальне рішення, яке

Середній виграш буде дорівнювати ціні гри V, яку б активну стратегію не використовував б гравець В. Для гри розміру 2x2 будь-яка чиста стратегія є активною, якщо сідлова точка відсутня. Виграш гравця А (програш гравця В) представляє собою випадкову величину, математичне очікування якої дорівнює ціні гри. Тому середній виграш гравця А (оптимальна стратегія) буде дорівнювати V для першої і другої стратегій гравця В.


Розв'язуючи систему (2.3.1), отримаємо значення шуканих ймовірностей
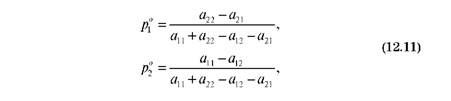
І ціни гри
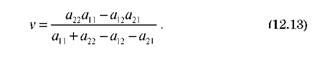

Використанні будь-якої чистої стратегії гравця А середній програш гравця В дорівнює ціні гри v, тобто
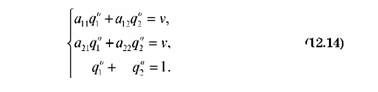
Звідки отримаємо значення шуканих ймовірностей
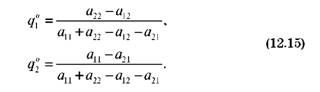
Приклад 12.4. Знайти рішення матричної гри, платіжну матрицю якої побудовано в прикладі 12.1.
Розв язаттття. Знайдемо нижню і верхню ціни гри за допомогою алгоритму знаходження максиміну (мінімаксу). В кожному рядку платіжної матриці знайдемо мінімальне з чисел aij і запишемо його у додатковий стовпчик minaij.
Таблиця 12.10 Платіжна матриця гри про вибір сторони монети

З найдених чисел виберемо найбільше за формулою (12.5) а = max ai = max {-1,-1} = -1, що визначає нижню ціну гри або максимін, тобто максимальний виграш, який гравець А може собі гарантувати в грі, що розглядається. Цей виграш відповідає стратегіям A1, A2. Тобто кожна стратегія фірми А є максимінною.
В кожному стовпці платіжної матриці знайдемо максимальне з чисел aij запишемо його у додатковий рядок max aij.
З найдених чисел виберемо найменше за формулою (12.6) ß = min ßj = min {1,1} = 1, що визначить верхню ціну гри або мі-німакс, тобто мінімальний програш, який гравець В може собі дозволити в грі, що розглядається, який відповідає стратегіям B1, B2. Ці стратегії є мінімаксними.



Розв язання. Скоротимо розмірність платіжної матриці. Стратегії А1 і А3 гравця А співпадають, тому виключимо стратегію А3:
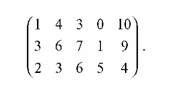
Стратегії В5, В3 і В2 гравця В домінують стратегію В1, тому їх можна виключити з платіжної матриці:

Стратегія А1, гравця А домінується стратегію А2, тому стратегію А1 можна виключити з платіжної матриці:
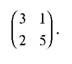
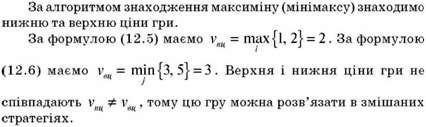

Схожі статті
-
Якщо матрична гра не має сідлової точки, то використання чистих стратегій не дає оптимального рішення гри. Так матрична гра, яку розглянуто у прикладі...
-
Визначимо найкращу стратегію гравця А з урахуванням всіх можливих відповідей на неї гравця В. При цьому слід розраховувати на те, що на будь-яку...
-
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 12.1. Матрична парна гра
12.1. Матрична парна гра Розглянемо антагоністичну парну скінченну матричну гру з нульовою сумою, в якій два гравця А і В. Інтереси гравців А і В прямо...
-
12.1. Матрична парна гра Розглянемо антагоністичну парну скінченну матричну гру з нульовою сумою, в якій два гравця А і В. Інтереси гравців А і В прямо...
-
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 11.2. Класифікація ігор
Теоретико-ігрові моделі класифікуються залежно від числа послідовних ходів і можливих способів дій гравців, характеру і обсягу інформації, що доступна...
-
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 3.5.1. Критерій Вальда
Критерій прийняття рішень - це функція, що виражає переваги особи, що приймає рішення, і що визначає правило, за яким вибирається прийнятний або...
-
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 3.5.2. Критерій оптимізму
Критерій прийняття рішень - це функція, що виражає переваги особи, що приймає рішення, і що визначає правило, за яким вибирається прийнятний або...
-
Критерій прийняття рішень - це функція, що виражає переваги особи, що приймає рішення, і що визначає правило, за яким вибирається прийнятний або...
-
РОЗДІЛ 11. Методологічні засади теорії ігр 11.1. Предмет теорії ігор Як і будь-яка людська діяльність, підприємництво обов'язково несе в собі елементі...
-
РОЗДІЛ 11. Методологічні засади теорії ігр 11.1. Предмет теорії ігор Як і будь-яка людська діяльність, підприємництво обов'язково несе в собі елементі...
-
Для обгрунтування господарських рішень Метод дерева рішень - це один з методів автоматичного аналізу величезних масивів даних. Перші ідеї створення...
-
Для обгрунтування господарських рішень Метод дерева рішень - це один з методів автоматичного аналізу величезних масивів даних. Перші ідеї створення...
-
Необхідність прийняття рішень в умовах невизначеності притаманна відносинам між суб'єктами господарювання. Повна (безнадійна) невизначеність означає...
-
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 11.1. Предмет теорії ігор
РОЗДІЛ 11. Методологічні засади теорії ігр 11.1. Предмет теорії ігор Як і будь-яка людська діяльність, підприємництво обов'язково несе в собі елементі...
-
Необхідність прийняття рішень в умовах невизначеності притаманна відносинам між суб'єктами господарювання. Повна (безнадійна) невизначеність означає...
-
Методологія - навчання про структуру, логічну організацію, методи і засоби діяльності. Методологія є необхідним атрибутом будь-якої прикладної науки, її...
-
Методологія - навчання про структуру, логічну організацію, методи і засоби діяльності. Методологія є необхідним атрибутом будь-якої прикладної науки, її...
-
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 3.6.1. Критерій Байєса
Якщо при ухваленні рішення ОПР відомі ймовірності Рj станів Пj, то будемо вважати, що розглядається ситуація в умовах часткової невизначеності. Гравець...
-
У даному розділі формулюються моделі прийняття рішень в умовах невизначеності. Особливістю цих моделей є їх нормативний характер. Вони дають змогу...
-
У даному розділі формулюються моделі прийняття рішень в умовах невизначеності. Особливістю цих моделей є їх нормативний характер. Вони дають змогу...
-
У даному розділі формулюються моделі прийняття рішень в умовах невизначеності. Особливістю цих моделей є їх нормативний характер. Вони дають змогу...
-
Якщо при ухваленні рішення ОПР відомі ймовірності Рj станів Пj, то будемо вважати, що розглядається ситуація в умовах часткової невизначеності. Гравець...
-
Якщо при ухваленні рішення ОПР відомі ймовірності Рj станів Пj, то будемо вважати, що розглядається ситуація в умовах часткової невизначеності. Гравець...
-
У випадку, коли ОПР орієнтується на найменш сприятливі умови та неконтрольовані фактори застосовують критерій песимізму. Для гри, яку задано матрицею...
-
У випадку, коли ОПР орієнтується на найменш сприятливі умови та неконтрольовані фактори застосовують критерій песимізму. Для гри, яку задано матрицею...
-
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 10.5.2. Стратегічний ризик
Кожний вид підприємницької діяльності передбачає розробку стратегій управління підприємством. Навіть відсутність довгострокової стратегії - це насправді...
-
10.4.1. Моделі управління ризиком Успішність діяльності суб'єктів господарювання значною мірою залежить від прийнятої концепції управління ризиками. Але...
-
10.4.1. Моделі управління ризиком Успішність діяльності суб'єктів господарювання значною мірою залежить від прийнятої концепції управління ризиками. Але...
-
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 3.5.3. Критерій песимізму
У випадку, коли ОПР орієнтується на найменш сприятливі умови та неконтрольовані фактори застосовують критерій песимізму. Для гри, яку задано матрицею...
-
Під невизначеністю розуміється наявність неповної інформації про умови прийняття господарських рішень, а не відсутність будь-якої інформації....
Обгрунтування господарських рішень та оцінювання ризиків - Донець Л. І. - 12.4. Розв'язування матричних ігор розміру 2x2