Менеджмент підприємства - Хомяков В. І. - В. Розв'язання задачі

А. Загальні положення симплекс-методу

Загальну методику симплекс-методу розглянемо на прикладі підприємства, до складу якого входять чотири виробничі цехи, де виготовляються два вироби 1 та 2. Виробничі потужності цехів (у годинах) у розрахунку на добу становлять відповідно: m1 = 12, m2 = 8, m3 = 16, m4 = 12.

Норми часу, необхідного для виготовлення одиниці продукції:

Цех

Норми часу (год/од.) для виробів

1

2

1

2

2

2

1

2

3

4

0

4

0

4

Як видно з наведених даних, для виготовлення одиниці виробу 1 потрібні 2 год. роботи першого цеху, 1 год. роботи другого цеху, 4 год, роботи третього цеху, а четвертий цех не бере участі у виготовленні виробу 1, Дня виготовлення одиниці виробу 2 необхідні 2 год. роботи першого цеху, 2 год. роботи другого цеху, 4 год. роботи четвертого цеху, а третій цех не бере участі у виготовленні виробу 2.

Прибуток від реалізації одиниці виробу 1 становить 2 тис. грн., а одиниці виробу 2-3 тис. грн. (цифри умовні). Слід обрати той із можливих варіантів виробничого плану, за якого забезпечується максимальний прибуток.

Позначимо через Х1 кількість виробу 1, а через Х2 - кількість виробу 2. Користуючись нормами часу та даними про виробничі потужності цехів, можемо стверджувати, що мають виконуватись умови:

Тому що можливі тільки такі варіанти виробництва, за яких не перевищуються виробничі потужності цехів.

Сумарний прибуток підприємства становить

Необхідно визначити такі обсяги виготовлення виробів 1 та 2, за яких досягається максимальний прибуток.

Введемо допоміжні змінні Х3, Х4, Х5, Х6, щоб мати рівняння

Допоміжні змінні означають невикористані виробничі потужності першого, другого, третього та четвертого цехів.

Симплекс-метод полягає в послідовному поліпшенні варіантів плану, аж до знаходження оптимального варіанта.

Першим і, очевидно, найменш вигідним, можна прийняти варіант плану, в якому Х1 = Х2 = 0. Тоді прибуток від продукції Z = 0, а виробничі потужності цехів зовсім не використовуються. Від першого варіанта можна перейти до другого - кращого, враховуючи в планах один із виробів; вигідніше ввести в план виріб 2, тому що він забезпечує більший прибуток на одиницю продукції.

Враховуючи норми часу, необхідні для виготовлення виробу 2 у відповідних цехах, можна встановити обсяг виробництва цього виробу. У першому цеху він становить 6 одиниць (12:2), у другому - 4 одиниці (8:2), а в четвертому - 3 одиниці. Допустимий обсяг виготовлення виробу 2 визначає четвертий цех.

Якби виріб 1 не виготовлявся, то за повного використання виробничих потужностей четвертого цеху (Х6 = 0) можна було б встановити план виробництва в обсязі Х2 - 3 од. Тоді прибуток становив

З рівняння (5.296) видно, що розмір прибутку Z можна збільшити за рахунок введення до плану виготовлення виробу 1 в обсязі Х1.

Числові коефіцієнти при невідомому Х1 в рівняннях (5.25a)-(5.27а) є нормами часу для виробу 1, а вільні члени показують виробничі потужності першого, другого та третього цехів, які вони ще мають. Таким чином, кількість виробів 1, яка може бути виготовлена в цих цехах, становить 3 одиниці (6:2) в першому цеху, 2 одиниці (2:1) в другому та 4 одиниці (16:4) в третьому. Допустимий обсяг виробництва виробу 1 визначає другий цех: Х1 - 2.

Так ми одержали другий, удосконалений варіант плану: Х1 = 2, Х2 = 3. Відповідний йому прибуток становить:

З рівняння (5.29в) видно, що величина, за допомогою якої можна збільшити розмір прибутку, є змінна А^, тобто невикористані потужності четвертого цеху. Обчислюючи частки від ділення вільних членів на додаткові коефіцієнти шостого стовпця рівнянь (5.25в), (5.27в), (5.28в), знаходимо: 2:(1/2) = 4, 8:2 = 4, 3:(1/4) = 12. Допустиме значення змінної Х$ можна знайти з рівняння (5.25в) або (5.27в). З рівняння (5.25й) знаходимо:

З рівняння (5.29г) видно, що в ньому немає жодної змінної, за допомогою якої можна було б збільшити прибуток 2, тому що коефіцієнти біля змінних у цьому рівнянні негативні. Прибуток досягає максимуму якраз тому, що Х3 = Х4 = 0 (будь-яке інше значення цих змінних зменшило б прибуток).

Підставляючи Х3 = X4 = 0 послідовно в рівняння (5.25г)-(5.29г), знаходимо: X6= 4, Х1 = 4,Х5 = 0, Х2 = 2, Z max = 14 тис. грн.

Таким чином, ми отримали найкращий варіант виробничого плану. Такий варіант передбачає виготовлення виробу 1 в кількості X1 = 4, виробу 2 - в кількості Х2 - 2. У випадку використання такого варіанта прибуток досягає максимуму (14 тис. грн.), причому для цього варіанта виробничі потужності першого, другого та третього цехів використовуються повністю {Х3 = Х4 = Х5 = 0), тоді як недовикористання виробничих потужностей четвертого цеху становить 4 одиниці.

На практиці описаний метод можна спростити, використавши матричний запис. Коефіцієнти при невідомих у системі рівнянь (5.25а)-(5.29я) можна записати у вигляді матриці АА. Оскільки ми шукаємо максимум Z, то стовпець, у якому цільова функція має найбільший коефіцієнт, приймаємо "обраним" і для того, щоб виділити його, обводимо його рамкою. Ділячи стовпець вільних членів на позитивні коефіцієнти "обраного" стовпця, знаходимо числа, що виписані справа від матриці АA. Виділимо рядок, у якому частка від цього ділення має найменше значення (це допустимий обсяг виробництва). Маємо матрицю використання виробничих потужностей.

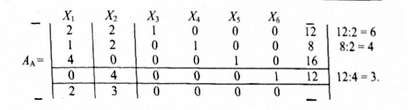
За допомогою виділеного рядка перетворимо матрицю АА так, щоб на перетині виділених рядка і стовпця одержати одиницю, а в інших рядках виділеного стовпця - нулі. Для цього достатньо четвертий виділений рядок матриці АА поділити на 4, а потім отриману частку помножити на (-2) і додати послідовно з першим і другим рядками, помножити на (-3) і додати з п'ятим рядком, а третій рядок залишити без змін. Після цих перетворень одержимо матрицю АБ.

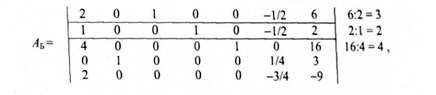
В якій обраний стовпець - перший, а обраний рядок - другий. Обведемо їх рамками. Справа від матриці - обчислені частки від ділення вільних членів на позитивні елементи обраного стовпця. Помноживши обраний рядок на (-2), додавши його послідовно з першим і п'ятим рядками, помноживши його на (-4) та додавши з третім рядком, перетворимо матрицю АБ таким чином, щоб в обраному стовпці всюди були нулі, окрім другого рядка, де повинна бути 1,0. Після цих перетворень одержуємо матрицю

Із останнього рядка матриці Ав видно, що наступним "обраним" стовпцем повинен бути шостий, а обраним рядком - перший або третій.

Після відповідних перетворень одержуємо матрицю Аг.

Із останнього рядка матриці Аг видно, що вже нема змінної, за допомогою якої можна було б збільшити значення цільової функції. Перетворення матриці закінчене.

Ті змінні, для яких в останньому рядку отримали негативні коефіцієнти, слід прирівняти до нуля (Хз = Х4= 0), а інші змінні обчислити з окремих рядків, кожен з яких є рівнянням з відповідними коефіцієнтами при невідомих, а в правій частині воно дано останнім

Зі сказаного стає зрозумілою така черговість етапів знаходження цільової функції симплекс-методом:

1. Нерівності змінюються рівняннями шляхом введення відповідних допоміжних змінних.

2. Задача записується у вигляді симплексної матриці.

3. Визначається змінна, яка має найбільший коефіцієнт у цільовій функції, а стовпець, що вміщує цю змінну, приймається як "обраний".

4. Визначається рядок, в якому результат ділення вільного члена на позитивний коефіцієнт "обраного" стовпця має найменше значення; цей рядок приймається як "обраний".

5. Оперуючи "обраним" рядком, перетворюємо вихідну матрицю так, щоб на перетині "обраних" стовпця і рядка отримати одиницю, а в інших рядках "обраного" стовпця - нулі.

6. Цю операцію повторюємо доти, доки в цільовій функції не одержимо лише непозитивні коефіцієнти.

7. Змінні, коефіцієнти яких негативні, приймаються як нульові (оскільки вони не збільшують цільову функцію).

8. Інші змінні розраховуються з рівнянь, відповідних останній матриці.

При використанні ЕОМ етапи 3-8 виконує обчислювальна машина. При цьому достатньо ввести в ЕОМ розрахункову матрицю, а потім роздрукувати і проаналізувати отримані результати.

Нижче розглянуті приклади розв'язання моделей лінійного програмування за допомогою ЕОМ.

Б. Вибір портфеля інвестицій

Клієнт доручив біржовому брокеру інвестувати значну суму грошей в портфель звичайних акцій. Мета - максимізація зростання капіталу. При цьому для обраного портфеля інвестицій ризик не повинен перевищувати заданої величини. Крім того, має бути забезпечений достатній прибуток, щоб сплатити податки і здійснити інші платежі. Біржовий брокер володіє інформацією про значну кількість компаній різних галузей промисловості. Кожна компанія ранжована за бальною шкалою від 0 до 9 за зростанням капіталу та потенційним ризиком. При цьому 0 означає відсутність зростання або ризику, а 9 - максимальні зростання або ризик. Крім того, не більше ніж 35% портфеля інвестицій можуть бути вкладені в будь-яку окрему галузь промисловості. Загальний коефіцієнт ризику не повинен перевищувати 10. Інформація про компанії наведена в таблиці 5.10.

Визначимо через Хі частку інвестиційного портфеля, який повинен бути вкладений в і-те підприємство. Тоді цільова функція може бути записана таким чином (зростання капіталу):

Таблиця 5.10. Характеристика підприємств

характеристика підприємств

Розв'язання матриці показує, що оптимальне значення цільової функції дорівнює 8,7. Оптимальне значення змінних 4, 8 та 16 дорівнює відповідно 0,35; 0,3; 0,35. Інші змінні дорівнюють нулю. Таким чином, для інвестицій обираємо підприємство 4 галузі А, підприємство 8 галузі Б та підприємство 16 галузі Г.

В. Розв'язання задачі

Припустимо, що підприємство виготовляє три вироби А, Б і В. При цьому використовуються два виробничі процеси - 1 і 2. На кожний виріб витрачається така кількість робочого часу (в годинах):

Виріб

Виробничий процес

1

2

А

9

11

Б

5

18

В

20

6

Розв'язання матриці показує, що максимум прибутку 1471 грн. за тиждень досягається при виробництві 33, 28 товарів А і 21, 94 товарів Б. При цьому виробництво товарів В повинне дорівнювати нулю.

Схожі статті




Менеджмент підприємства - Хомяков В. І. - В. Розв'язання задачі

Предыдущая | Следующая