Страхування - Базилевич В. Д. - 24.2. Інтенсивність смертності

Використовуючи формулу (24.3), отримаємо щільність ймовірності смерті після досягнення віку х. Підставимо у формулу (24.3)2 = *+ Ах

Р(х<Хїх + Ах/Х>х) = Р*ІХ + ^)-Р*Іх)*М^. (24.12)

У цьому виразі FX(x) = fX(x) - щільність неперервної ви-

F(x)

Падкової величини X, "вік у момент смерті". Функція --

(1-.?(*)..

У формулі (24.12) може інтерпретуватися в термінах умовної щільності. Для кожного віку х вона дає значення в точці Х Умовної функції щільності випадкової величини X За умови дожиття до віку Х І позначається через і(х). Тоді

MW-T^ff^- <2413)

L-FX(x) s(x)

З властивостей функцій fX(x) і 1-F(x) маємо, що ц(д:)>0.

У актуарній науці і в демографії И(х) називається інтенсивністю смертності. У теорії надійності, яка досліджує ймовірності безвідмовної роботи механізмів і систем, ця величина називається інтенсивністю відмов.

Як і функція дожиття, інтенсивність смертності може використовуватися для визначення розподілу випадкової величини X. З формули (24.13) для будь-якого додатного У маємо рівність для диференціалів

-u(y)dy = dlns(y). Інтегруючи цей вираз від х до Х + п, одержимо

Х+П / v

F / j і S (X + n) , - І u(y)dy = ln--L = NPx.

Тоді

X+n

ВР, = ехр{- \x(y)dy). (24.14)

X

Іноді зручно переписати формулу (24.14), зробивши заміну T = у - х:

П

П РХ =ехр{- Ji(x+t)dt}. (24.16)

О

Зокрема ми змінимо позначення з тим, щоб вони відповідали використаним у формулі (24.6), поклавши вік осіб, що вже жили, таким, що дорівнює 0, і позначивши вік дожиття через х. Тоді одержимо

X

ХРо = S(x) = ехр{- Ju(r)d*}. (24.16)

О

Крім того,

РХ (*) = 1 - а(х) = 1 - ехр{- |ц(г)Л} (24.17)

О

І

Х

(*) = ехр{-|ц(0Л>Ц<*)=, Ро И". (24.18) о

Нехай іг(Ж)(г) і позначають відповідно функцію роз-

Поділу і щільність Т(х), тривалості майбутнього життя особи (х). Помітимо, що 2^,(0 =і Ч" (див. позначення (24.4)). Таким чином,

/Т(х,(0=-Г ИЯХ)= - 1--=

ЙІ ОХ. 8(Х) .

, , У (24.19)

А(х+г)[ 8'(х+*))

8{х) у В(л;+г)>

Отже, ІРХЛ(х + І)йЧ є ймовірністю того, що особа (х) помре у

Віці між гИ + йЬ. Очевидно, що ІіРЖИ(х +*)Л = 1.

О

Формулу (24.19) можна подати у такому вигляді:

~а-А)-~(А)-.^*+*). (24.20)

Оскільки Ііт,,^ ПРХ=0, маємо Ііт^^-Іп ПРХ) = - ко. Таким чином,

Х+л

Ііт ( и(і/)гіі/ = +оо.

Л->оо * X

Використовуючи наступну формулу теорії ймовірностей Р(А^В)=Р(А)+Р(А)Р(В/ А), де А - доповнення до події А, отримаємо корисну формулу. Нехай А = {Г(дс)^г}, £ = {*<Т(х)£1},0<г<1. Тоді Р(АиВ)=Р(Т(х)й1)=ЯЯ, і)(А)=ІД"аР(В/А)=И дЖ+г

Отже, дХ = ІД" + <РХ1_ІДЖ+<.

X

24.3. Таблиці смертності

Таблиця смертності містить розташовані за віком індивідуумів значення основних функцій dX і, можливо, додаткових функцій, які можна отримати з них. Перш ніж навести таку таблицю, розглянемо інтерпретацію таких функцій, яка безпосередньо пов'язана з ймовірнісними функціями, що обговорювалися в попередньому розділі.

Згідно з формулою (24.9) умовна ймовірність того, що особа (х) помре протягом г років, обчислювалась так:

8(Х + І)

*?*=1-ІГТ~

S(x)

І, зокрема,

S(x + l)

А Х=1 --7~Г'

S(x)

Розглянемо тепер групу з 10 новонароджених, поклавши, наприклад, ^=100000.

Для кожного новонародженого випадкова величина "вік у момент смерті" має розподіл, заданий функцією дожиття $(х). Позначатимемо через Цх) кількість осіб у групі, що дожили до віку х. Припишемо всім особам в групі номери / = 1,2,..., і помітимо, що

Де /, - індикатор дожиття особи з номером ], тобто

Г1, Якщо особа з номером j доживе до віку X, ' 10, Інакше.

K

Оскільки Jkf[/j] = e(x), то M[L(x)]=Јm[//] = /0S(x).

Нехай lX = M[L(x)]. Тобто ІХ - математичне сподівання кількості осіб, що дожили до віку Х З /0 новонароджених, і

K = k s(x). (24.21)

Далі, в припущенні, що індикатори Ij взаємно незалежні, L(x) має біноміальній розподіл з параметрами П = ІЬ І p~s{x).

Зазначимо, проте, що в рівнянні (24.21) не використовувалося припущення про незалежність.

Аналогічно позначимо через " ЛХ кількість померлих у віці між х і Х + п З початкової сукупності, що складається з людей. Нехай ПГіВ ЯЛ^["І)Я1. Оскільки для новонародженого ймовірність смерті у віці між х і х + п дорівнює 5(дг)-а(ж + л), використовуючи міркування, що наводилися вище щодо ІХ Отримаємо

"^ = М["І),]=і0[5(х)-8(лс + л)]=ІХ-І"". (24.22)

Якщо п = 1, то опустимо лівий нижній індекс у виразах "І)Я і ПЙХ. З формули (24.21) видно, що

І Аі* - 1 " йх~

ІХ ах з(х) dx - dlX =lXI(x)dx.

(24.23) (24.24)

Оскільки

Співмножник ІХХ(х) у (24.24) можна інтерпретувати як очікувану щільність смертей у віковому інтервалі (х9 x + dx). Зазначимо, що

/Х=4,-ехр

**+"=**-ехр

О

С+л

(24.25) (24.26) (24.27)

Для зручності посилань назвемо групу з ^ новонароджених, кожен з яких має функцію дожиття з(х), сукупністю випадкового дожиття.

Нижче наведено таблицю смертності населення Тернопільської області віком до 10 років1 (табл 24.1). Функції $Х, DX та о/Л в цій таблиці представлені для ^ =100000. Подібні таблиці не створюються на основі спостереження за 100 000 новонароджених аж до смерті останнього з них, а грунтуються на оцінках

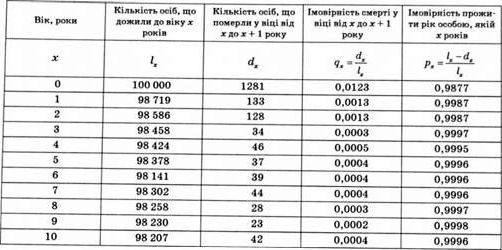
Ймовірності смерті за умови дожиття до різного віку на основі даних про смертність населення у відповідні роки. Ілюстративні таблиці смертності наведені в деяких роботах1. Зробимо деякі зауваження щодо таблиці.

1. Очікується, що близько 1 % новонароджених, які входять до сукупності дожиття, помруть на першому році життя.

2. До віку 10 років доживе більше 98 % із групи новонароджених.

3. Відносне збільшення кількості смертей очікується для віку 4, 7 та 10 років.

4. Хоча значення ІХ було округлено до цілих чисел, відповідно до формули (24.21) це робити не обов'язково.

Таке представлення, як у цій таблиці, є стандартним методом опису розподілу віку в момент смерті. Іншим способом є представлення функції дожиття в аналітичній формі, наприклад в(л:) = е-еж, с>0, Х> 0. Однак більшість досліджень смертності для потреб страхування використовує вираз 8(х) =-.

Оскільки величина 100 000 Б(х) Представлена лише для цілих значень Ху При обчисленні в(х) для нецілих значень аргументу необхідно використовувати інтерполяцію.

Приклад 24.1. Використовуючи таблицю, обчислити ймовірність того, що особа у віці трьох роки:

1) доживе до віку 10 років;

2) помре, не доживши до віку 8 років;

3) помре між 6 та 9 роками.

Згідно з формулою (24.8), ймовірність того, що особа віком трьох років доживе до 10 років, дорівнює £&;0)=К=^ 5.

8 (3) /з 98 458 Згідно з формулою (24.9), ймовірність того, що особа віком З роки не доживе до віку 8 років, дорівнює *3)-*(8ИА = 1_98258

8(3) /з 98458

Згідно з формулою (24.10), ймовірність того, що особа віком 3 роки помре між 6 та 9 роками, дорівнює

В(6)-в(9) ^-^ 98341-98230

=0,0011

В(3) і, 98 458

Перейдемо тепер до другої, неймовірнісної, інтерпретації таблиць смертності. Вона за природою детерміністична і приводить до поняття сукупності детермінованого дожиття, або Когорти.

Сукупність детермінованого дожиття, як видно з таблиці смертності, має такі характеристики:

O спочатку складається з ^ осіб віку 0;

O для членів сукупності в будь-якому віці діють фактичні річні коефіцієнти смертності (вибуття), які визначаються величинами дХ в таблиці смертності;

O сукупність є замкнутою. До неї не може входити ніхто, крім тих ¿0 осіб, які були в ній на самому початку. Вихід із цієї сукупності обумовлений фактичними річними коефіцієнтами смертності (вибуття) і лише ними.

З наведених вище характеристик маємо

А =*о(1-?.)Ч-<*о.

*г=1| (!-",)=*,-<*, =4-(4,+<*.).

='х-. (1-?.-.)=^, -<*,-, = *> "і/*"

І,=о

*о у=о,

(24.28)

Де ІХ позначає число осіб, що дожили до віку х у сукупності дожиття. Число ¿0 називається коренем таблиці смертності. Ці рівності можна переписати так:

*2=кРі=0"Ро)Рі*

К=К -уРх -1=к

Пл

(24.29)

720

Між сукупністю детермінованого дожиття і моделлю складних відсотків є аналогія, деякі положення якої підсумовуються в табл. 24.2.

Таблиця 24.2. Поняття теорії складних відсотків і відповідні їм поняття в теорії сукупностей детермінованого дожиття

Заголовки до стовпців табл. 24.1 для ІХ*оІХ, дХ9 рХ Належать до сукупності детермінованого дожиття. Хоча математичні основи для сукупностей випадкового і детермінованого дожиття різні, функції ІХ, <іХ, 5Х, рХ мають однакові математичні властивості і аналізуються однаково. Поняття сукупності випадкового дожиття має перевагу в тому, що воно дає змогу користуватися усім апаратом теорії ймовівностей. Сукупність детермінованого дожиття концептуально простіша і її легше використовувати, хоча вона не відображає випадкових коливань чисельності тих, хто дожив до певного віку.

Далі отримаємо вирази для основних числових характеристик розподілів випадкових величин Т(х) і К(х) і виведемо загальний метод обчислення деяких з цих характеристик.

Математичне сподівання Т(х), що позначається через ЕХ, Називається повною очікуваною тривалістю життя. Використовуючи формулу (24.20), отримаємо

00

Ех = Аї [Т( х)] = J* o ,pjix+t)d t =

0 (24.30)

00 00

= f*4(-,a)-*-(-,p,)t +*-,Р***-

0 0

З існування M[T(x)] випливає співвідношення Mmt-(-TPX) = 0. Таким чином,

І-мо

Z = ),P, dt- (24.81)

0

Повна очікувана тривалість життя у різному віці часто використовується для порівняння рівнів охорони здоров'я країн.

Аналогічно підраховується другий момент:

00 00

М[Т(дс)Г] = іГ ■ ,рХіХ(х+t)dt = 2 ■ TPlDt.

0 0

Тоді дисперсія дорівнює

Л[Г(*)] = М[Г(*)1]-(М[Г(*)])2 =2j* ,P ,dtMX)

О * '

Медіану тривалості майбутнього життя особи {х)9 яка позначається через Т(х), можна знайти як розв'язок рівняння

Р(г(х)>т(*))4 або *("*у> Л 2 s(*) 2

Відносно m(x). У конкретному випадку тп(0) є розв'язком рівняння s(m(0)) = l/2.

Модою розподілу випадкової величини Т(х) буде те значення T, за якого значення функції TPXU(x+t) буде максимальним.

Математичне сподівання випадкової величини К(х) позначається через ЕХ. Ця величина називається покроковою очікуваною тривалістю життя. Ті числові характеристики дорівнюють:

■*" 00 00 00

ЕХ = M[K]=^k- KPxQ"K = Y,4KPX - MPA) = Y,^iPx=Y, kPx

*=0 *=0 *=0 H 1

М[ЛГ(*)2] = £*2 o К Р, д", = £(2Л+1)- МРг =£(2Л-1)- ,р,;

*=0 *=0 я=1

ВД = М[ЛГЇ]-(М [А"])' = ¿(2/8-1) ІЛ -4.

Символ ЬХ означає загальну очікувану кількість років, прожитих між віком Х Та Х + 1 особами з цієї групи, що містить /0 новонароджених, які дожили до віку х. Тоді

00

0

Де інтеграл у правій частині дорівнює числу років, прожитих тими, хто помер у віковому інтервалі між Х Та Х +1, а ІХ+1 дорівнює числу років, прожитих у віковому інтервалі між Х Та Х + 1 тими, хто дожив до віку Х + 1. Інтегрування частинами дає і і і

Ь" - - * o +Ь + +'"і =

0 0 0

Функція ЬХ також використовується при визначенні вікового коефіцієнта смертності в інтервалі між х і Х + 1, який позначається через тХ, де

І

Т _ 0 _ *х *дг+1

0

Наведені вище визначення для ТХ І ЬХ Можна поширити на вікові інтервали довжиною більшою від одиниці.

П п

"ьх =- І ■ Імі(х+Ті +П ■ і"я=Імйі,

О

П

[і^ріх+фЛ О

Для сукупності випадкового дожиття П ЬХ є загальною очікуваною кількістю років, прожитих у віковому інтервалі між Хіх + п для осіб, що дожили до віку Х з вихідної групи, що містить /о новонароджених, а П ТХ є віковим коефіцієнтом смерт

0

П

M =4--=Л

Ності, що можна спостерігати для цієї групи на інтервалі (х, х + п).

Символ ТХ означає загальну кількість років, прожитих після досягнення віку Х Особами, що дожили до цього віку з вихідної групи, яка має ^ новонароджених. Маємо

00 00 00

0 0 0

Останній вираз можна інтерпретувати як інтеграл від загального часу, прожитого між віком х + гіх + * + Л групою з ІХ+І осіб, що дожили до цього вікового інтервалу. Звернемо також увагу, що ТХ Є межею величини ЛЬХ> коли П прямує до нескінченності.

Середня кількість років майбутнього життя для ІХ Осіб з групи, що дожили до віку Х, визначається виразом

Т }"* - г o

*дс *х 0

Відповідно до формул (24.30) і (24.31).

Знайдемо вираз для середньої кількості років, прожитих між віками х і х + п групою з ІХ осіб, що дожили до віку Х:

Я

Т JХ+< т - Т

І " / " І -}*Р*'

ІХ іХ ьХ 0

Ця функція є зрізаною (на п - річному інтервалі) повною

Очікуваною тривалістю життя Для осіб (х) і позначається о

Через ЄхЯ.

Останньою функцією, пов'язаною з інтерпретацією таблиці смертності, є середня кількість років, прожитих між віком X Та Х + 1 тими особами в групі, що дожили до віку х, які вмирають у деякий момент між цими віками. Ця функція позначається через а(х) і визначається співвідношенням

І

А(ж)-*,-.

ІХиИ(х + і)(іі о

За ймовірніснісного погляду на таблиці смертності отримали б і

/*'іАЦ(*+*)Л А(х)=±1 -= М[Т/Т<1].

О

Якщо припустити, що ІХ+І х(х + ї)сІЇ = <іХ(Іі, 0 < £ < 1, тобто моменти смерті рівномірно розподілені всередині річного вікового інтервалу, то отримаємо

А(х)= ]*<** = -.

О *

Це звичайне наближення функції а(х), придатне для осіб різного віку, окрім зовсім юних і дуже старих, де це припущення може не відповідати дійсності.

Справедлива рівність ЬХ =а(х)ІХ +

24.4. Деякі аналітичні закони смертності

У табл. 24.3 наводяться кілька сімейств простих аналітичних функцій смертності й дожиття, що відповідають різним відомим законам. Для зручності посилань наведені назви законів, що лежать у їхній основі, і дати публікації.

Зазначимо такі факти:

O спеціальні символи визначаються формулами Т =-,

И~-;

+ Т "

O закон Гомперца є контактним випадком закону Мейке-

Ма при А = 0;

O якщо с = 1 у законах Гомперца й Мейкема, то отримаємо експонеціальний (постійна інтенсивність смертності) розподілу;

O доданок А у законі Мейкема не залежить від віку і відповідає смертності від нещасних випадків, у той час як доданок ВсХ описує вплив віку на смертність (старіння) і в цьому сенсі відповідає смертності від "природних" причин.

Таблиця 24.3. Функції смертності й дожиття для різних розподілів

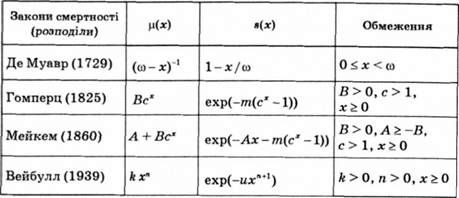
Нижче зібрано основні поняття, згадані в цьому розділі, відповідні терміни, позначення й описи (табл. 24.4).

Таблиця 24.4. Основні позначення розділу 24

Закінчення табл. 24.4

Висновки

1. У цьому розділі розглянуто основні моделі тривалості життя. Основними елементом цих моделей є тривалість майбутнього життя.

2. Роглянуто основні ймовірностні характеристики моделі тривалості життя: функція дожиття, ймовірності смерті, по-крокова тривалість майбутнього життя.

3. Важливою характеристикою моделі тривалості життя є інтенсивність смертності.

4. Незамінним компонентом багатьох моделей актуарної математики є таблиці смертності.

5. Між сукупністю детермінованого дожиття і моделлю складних відсотків є аналогія.

6. У законах смертності Гомперца й Мейкема найчастіше використовуються в моделях тривалості життя.

Навчальний тренінг

Основні терміни і поняття

Тривалість майбутнього життя; функція дожиття; покро-кова тривалість майбутнього життя; інтенсивність смертності; таблиці смертності; сукупність випадкового дожиття; сукупність детермінованого дожиття; корінь таблиці смертності; повна очікувана тривалість життя; покрокова очікувана тривалість життя; віковий коефіцієнт смертності; зрізана повна очікувана тривалість життя; закони смертності; закон Гомперца; закон Мейкема.

Схожі статті




Страхування - Базилевич В. Д. - 24.2. Інтенсивність смертності

Предыдущая | Следующая